Question
Question: A popular game in India is goli which is played with small glass balls called golis. A goli of one p...
A popular game in India is goli which is played with small glass balls called golis. A goli of one player is situated at a distance of 2 m from the goli of the second player. The second player has to project his goli by keeping the thumb of the left hand at the place of his goli, holding the goli between his two middle fingers and making the throw. If the projected goli hits the goli of the first player, the second player wins. If the height from which the goli is projected is 19.6 cm from the ground and the goli is to be projected horizontally, with what speed should it be projected so that it directly hits the stationary goli without falling on the ground earlier?
Solution
Hint: A goli thrown horizontally from a height ‘h’ will have a horizontal as well as vertical component of velocity. The velocity of projection should be sufficient in order to reach the other goli 2 m away on the ground.
Complete step by step answer:
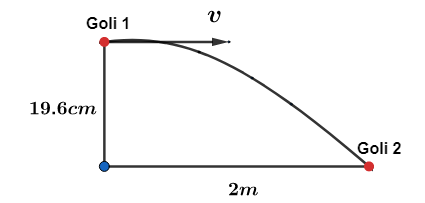
So when a goli is projected from a height with velocity in the horizontal direction, it will be accelerated downwards due to the acceleration due to gravity acting on it. So the goli will eventually fall to the ground due to gravity. The time it takes for the goli to fall to the ground is given by,
T=g2h
Where, h is the height from which goli is projected, 0.196 m in our case.
g is the acceleration due to gravity.
T is the time taken to reach the ground.
So substituting the values in the equation we get,
T=9.82×0.196
T=0.2 seconds
So the horizontal velocity needed to cover the distance of 2 m before the ball reaches the ground is.
Velocity(VH)=TimeDistance
VH=0.22
VH=10 m/s
So the goli should be projected horizontally with a velocity of 10 m/s in order to hit the second goli directly.
Note:
The goli is under free fall in the y-axis or the vertical direction due to gravity acting along the vertical direction. The body is accelerated along the y-axis, but it is not accelerated along the x-axis.
Decrease or increase in the horizontal velocity as calculated from the problem will result in missing the target. If the velocity is increased from the required velocity, the goli will overshoot the target, and if it is decreased, it will fall before it reaches the target.
