Question

A political party has to start its procession in an area where wind is blowing at a speed of $30\sqrt 2 \,Km{h^{ - 1}}$ and party flags on the cars are fluttering along the north-east direction. If the procession starts with a speed of $40\,Km{h^{ - 1}}$ towards north, find the direction of flags on the cars.

Answer 1

Here we are provided with the direction and the velocity of the car moving and the wind blowing. We have to use the vector method to get the direction of the flag placed on the car. The resultant vector of the flag by the virtue of motion of car and wind respectively. We’ll get the resultant direction of the flag.

Complete step by step answer:
The above question is of vectors. We have to find the direction of the flags of car, conditions provided that the car is moving towards north direction with the speed of $40\,Km{h^{ - 1}}$ and the wind is blowing in the north-east direction with the speed of $30\sqrt 2 \,Km{h^{ - 1}}$.

We have a vector representing the direction of the car towards the north direction as $\overrightarrow {{v_c}}$. So the direction of the flag waving by the virtue of the motion of the car will be exactly opposite to that of the vector of the car and will be given as $- \overrightarrow {{v_c}}$. Vector representing the direction of the wind blowing towards the north-east direction is represented as $\overrightarrow {{v_w}}$. Vector representing the resultant direction of the flag is $\overrightarrow {{v_{wc}}}$.

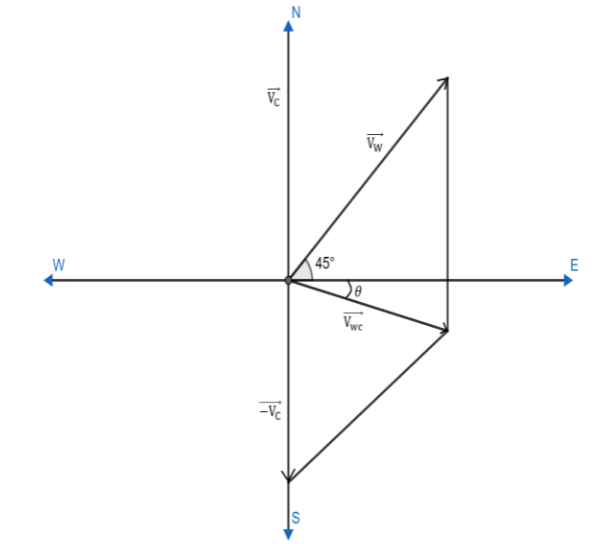
Angle made by $\overrightarrow {{v_w}}$ is $45^\circ$ with the positive direction of east direction. $\theta$ is the direction of the resultant vector by the parallelogram rule of vector addition and is directed as south of east. Now as $\overrightarrow {{v_w}}$ is in north east direction so the vector will be represented by the two components cos and sin also $\overrightarrow i$ and $\overrightarrow j$ respectively for the x component and y component and so $\overrightarrow {{v_w}}$ is given as,
$\overrightarrow {{v_w}} = \,30\sqrt 2 \cos 45^\circ \overrightarrow i \, + \,30\sqrt 2 \sin 45^\circ \overrightarrow j$

The vector $- \overrightarrow {{v_c}}$is towards y axis and hence the vector representing the direction of waving of flag by the virtue of motion of car is given by,
$- \overrightarrow {{v_c}} \, = \, - 40\overrightarrow {\,j}$
Now by the parallelogram rule of addition of vectors we’ll get the direction of flag as,
$\overrightarrow {{v_{wc}}} \, = \,\overrightarrow {{v_w}} - \overrightarrow {{v_c}}$
Substituting the values we get

\Rightarrow \overrightarrow {{v_{wc}}} = 30\sqrt 2 \dfrac{1}{{\sqrt 2 }}\overrightarrow i \,\, + \,\,30\sqrt 2 \dfrac{1}{{\sqrt 2 }}\overrightarrow {j\,} \, - \,40\overrightarrow j \\\ \Rightarrow \overrightarrow {{v_{wc}}} = \,30\,\overrightarrow i \, - \,10\overrightarrow j \, \\\ $$ Now for the required angle we have$$\tan \theta $$ is the ratio of the y component to the x component of the vector $$\overrightarrow {{v_{wc}}} $$ Now hence we have $$\tan \theta \, = \,\dfrac{{10}}{{30}}\,\, = \,\,\dfrac{1}{3}$$ Which gives $$\therefore \theta = {\tan ^{ - 1}}\dfrac{1}{3}$$ South of east **Hence the flag will flutter in a direction $$\theta = {\tan ^{ - 1}}\dfrac{1}{3}$$ south of east.** **Note:** We may also be asked to get the magnitude of the speed by which the flag is waving, we can obtain this by simply adding the magnitudes of the vector. One must be careful regarding the difference between the vector which represents the direction of the car and the vector representing the direction of the flag by virtue of the motion of the car as the flag is placed on the car itself.