Question

A police jeep, approaching a right-angled intersection from the north, is chasing a speeding car that has turned the corner and is now moving straight east. When the jeep is $0.6{\text{ km}}$ north of the intersection and the car is $0.8{\text{ km}}$ to the east, the police determine with radar that the distance between them and the car is increasing at $20{\text{ km/h}}$ . If the jeep is moving at $60{\text{ km/h}}$ at the instant of measurement, what is the speed of the car?

Answer 1

Analyse the given information and draw a diagram using that. Assign a variable ‘x’ to the distance of the car from the corner, ‘y’ to the distance of the jeep from the corner, and ‘s’ to the distance between car and jeep. Now use Pythagoras theorem to get the equation ${s^2} = {x^2} + {y^2}$ . Now differentiate this equation and find an expression for the $\dfrac{{dx}}{{dt}}$ , which will represent the speed of the car. Substitute the value to calculate the required value.

Complete step-by-step answer:
Here in this problem, we are given a condition where a police jeep is chasing a car. The jeep is coming from the North direction and the car has already taken a right-angle turn ahead of it. When the jeep is $0.6{\text{ km}}$ north of the intersection and the car is $0.8{\text{ km}}$ to the east, then the car is going towards the East direction and its speed is increasing at a rate of $20{\text{ km/h}}$ . With this information, we need to find the speed of the car at that instant.
Let’s draw a figure of the given information and assume that the distance of the car from the corner is ‘x’ and the distance of the jeep from the corner is ‘y’ at a time ‘t’.

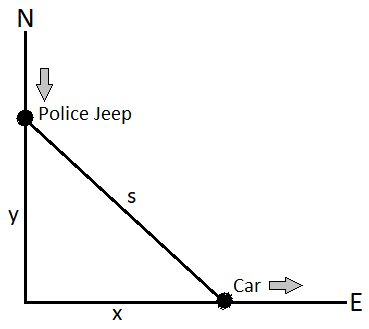
At the given instant, values are $x = 0.8km$ , $y = 0.6km$
Before starting with the solution we must understand the concept of differentiation. In mathematics (particularly in differential calculus), the derivative is a way to show the instantaneous rate of change: that is, the amount by which a function is changing at one given point. For functions that act on the real numbers, it is the slope of the tangent line at a point on a graph. The derivative is often written as $\dfrac{{dy}}{{dx}}$ ("$dy$ over $dx$ ", meaning the difference in y divided by the difference in x). The d is not a variable, and therefore cannot be canceled out.
Therefore, the rate of increasing distance between car and jeep can be represented as:
$\Rightarrow \dfrac{{ds}}{{dt}} = 20km/h$
Similarly, the decreasing distance of the jeep from the corner can be written as:
$\Rightarrow \dfrac{{dy}}{{dt}} = - 60km/h$ (negative because the value of ‘y’ is decreasing with respect to time)
According to the Pythagoras theorem, it states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
$\Rightarrow {x^2} + {y^2} = {s^2}$
Let’s differentiate the above equation with respect to the time ‘t’, we get:
$\Rightarrow \dfrac{{d\left( {{s^2}} \right)}}{{dt}} = \dfrac{{d\left( {{x^2}} \right)}}{{dt}} + \dfrac{{d\left( {{y^2}} \right)}}{{dt}}$
As we know, that the square of a square function is given by $\dfrac{{d\left( {{y^2}} \right)}}{{dx}} = 2y \times \dfrac{{dy}}{{dx}}$ . Using this in the above equation, we get:
$\Rightarrow \dfrac{{d\left( {{s^2}} \right)}}{{dt}} = \dfrac{{d\left( {{x^2}} \right)}}{{dt}} + \dfrac{{d\left( {{y^2}} \right)}}{{dt}} \Rightarrow 2s \times \dfrac{{ds}}{{dt}} = 2x \times \dfrac{{dx}}{{dt}} + 2y \times \dfrac{{dy}}{{dt}}$
Now we can divide both sides by $2$ and find the expression for $\dfrac{{ds}}{{dt}}$
$\Rightarrow \dfrac{{2s \times \dfrac{{ds}}{{dt}}}}{2} = \dfrac{{2x \times \dfrac{{dx}}{{dt}} + 2y \times \dfrac{{dy}}{{dt}}}}{2} \Rightarrow s\dfrac{{ds}}{{dt}} = x\dfrac{{dx}}{{dt}} + y\dfrac{{dy}}{{dt}} \Rightarrow \dfrac{{ds}}{{dt}} = \dfrac{1}{s} \times \left( {x\dfrac{{dx}}{{dt}} + y\dfrac{{dy}}{{dt}}} \right)$
Since we have the value of ‘s’ as ${s^2} = {x^2} + {y^2} \Rightarrow s = \sqrt {{x^2} + {y^2}}$. We can use this in the above equation
$\Rightarrow \dfrac{{ds}}{{dt}} = \dfrac{1}{s} \times \left( {x\dfrac{{dx}}{{dt}} + y\dfrac{{dy}}{{dt}}} \right) = \dfrac{1}{{\sqrt {{x^2} + {y^2}} }}\left( {x\dfrac{{dx}}{{dt}} + y\dfrac{{dy}}{{dt}}} \right)$
Therefore, we got the equation as $\dfrac{{ds}}{{dt}} = \dfrac{1}{{\sqrt {{x^2} + {y^2}} }}\left( {x\dfrac{{dx}}{{dt}} + y\dfrac{{dy}}{{dt}}} \right)$
Now we can substitute the already known values, i.e. $x = 0.8km$ , $y = 0.6km$ , $\dfrac{{ds}}{{dt}} = 20km/h$ and $\dfrac{{dy}}{{dt}} = - 60km/h$ ; and find the unknown value of $\dfrac{{dx}}{{dt}}$
$\Rightarrow \dfrac{{ds}}{{dt}} = \dfrac{1}{{\sqrt {{x^2} + {y^2}} }}\left( {x\dfrac{{dx}}{{dt}} + y\dfrac{{dy}}{{dt}}} \right) \Rightarrow 20 = \dfrac{1}{{\sqrt {{{0.8}^2} + {{0.6}^2}} }}\left( {0.8 \times \dfrac{{dx}}{{dt}} + 0.6 \times \left( { - 60} \right)} \right)$
Now putting the values of squares ${0.8^2} = 0.64{\text{ and }}{0.6^2} = 0.36$ and solving it further, we get:
$\Rightarrow 20 = \dfrac{1}{{\sqrt {0.64 + 0.36} }}\left( {0.8 \times \dfrac{{dx}}{{dt}} - 36} \right) \Rightarrow 20 = \dfrac{1}{{\sqrt 1 }}\left( {0.8 \times \dfrac{{dx}}{{dt}} - 36} \right)$
We can transpose the constants to one side and the unknown to the other
$\Rightarrow 20 = \dfrac{1}{{\sqrt 1 }}\left( {0.8 \times \dfrac{{dx}}{{dt}} - 36} \right) \Rightarrow 20 + 36 = 0.8 \times \dfrac{{dx}}{{dt}} \Rightarrow \dfrac{{dx}}{{dt}} = \dfrac{{20 + 36}}{{0.8}}$
Therefore, we get the required value as $\dfrac{{dx}}{{dt}} = \dfrac{{56}}{{0.8}} = 70$
Thus, the rate of increasing distance ‘x’ of the car from the corner or the speed of the car is $70km/h$.

Note: In questions like this, the understanding of differentiation always plays a crucial role in the solution. The symbol $\dfrac{{dy}}{{dx}}$ is used to represent the derivative of ‘y’ with respect to ‘x’ or the rate of change of ‘y’ with respect to ‘x’. Here letter ‘d’ is not a variable and cannot be canceled out. The letter ‘d’ means delta, which stands for small change.