Question
Question: A pole of height \(4m\) is kept in front of a vertical plane mirror of length \(2m\). The lower end ...
A pole of height 4m is kept in front of a vertical plane mirror of length 2m. The lower end of the mirror is at a height of 6mfrom the ground. The horizontal distance between the mirror and the pole is 2m. Up to what minimum and maximum heights a man can see the image of the top of the pole at a distance of 4m standing on the same horizontal line which is passing through the pole and the horizontal point below the mirror?
Solution
A plane mirror reflects light in such a way that the angle of incidence is equal to the angle of reflection. Since the horizontal distance of the man, mirror and pole is fixed, the maximum and the minimum angle of incidence also have a definite value, which could be found by joining the top of the pole to the ends of the mirror.
Complete step by step answer:
Given that-
Height of pole=4m
Length of the mirror=2m
Height of the lower end of the mirror= 6m
Horizontal distance between the mirror and pole=2m
Horizontal distance of man from the mirror=4m
For minimum distance-
Let the minimum angle of incidence and reflection beϕ.
In triangles, PQS and QOT the angleϕ is made, thus they are similar.
For triangle PQS,
tanϕ=OTQT
QT is the distance between the top of the pole and the lower end of the mirror. It is equal to 2m.
OT is the horizontal distance between pole and the mirror it is equal to 2m.
Therefore,
tanϕ=22=1
Angle of incidence,ϕ=45∘
We know that tanϕ=1
In triangle, PQS ,
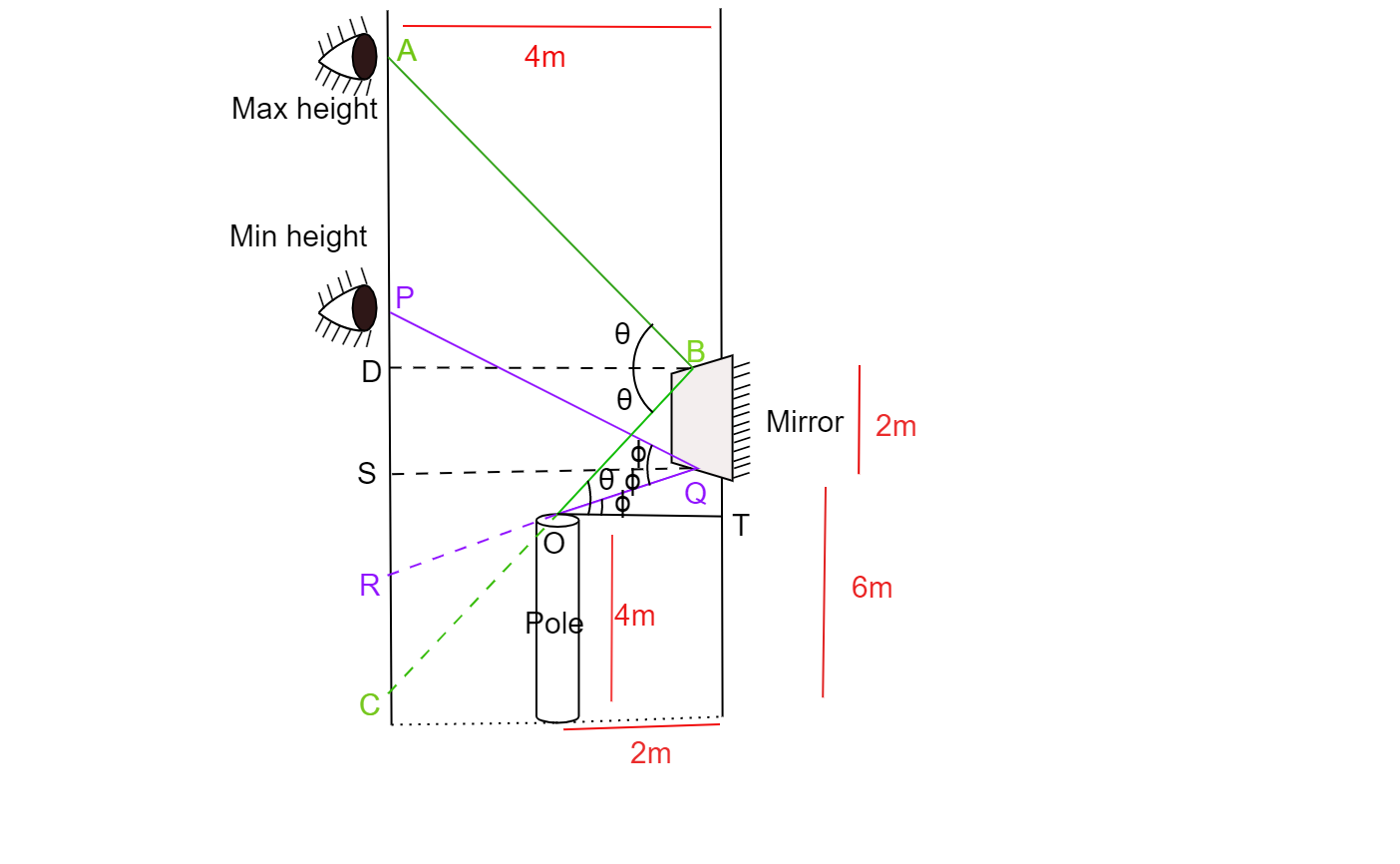
tanϕ=SQPS
Given, SQ=4
Therefore, PS=SQtanϕ
PS=4×1
PS=4m
The minimum vertical distance6+4=10m
For maximum distance-
Let the maximum angle of incidence and reflection be θ
In triangle BOT,
The angle O is equal to θ.
Thus, tanθ=OTBT=OTBQ+QT
tanθ=22+2=24=2
tanθ=2
Given, DB=4m
In triangle ABD,
tanθ=DBAD
Therefore, AD=DBtanθ
AD=4×2=8m
The maximum vertical distance =6+2+8=16m
The minimum distance where man can view the top of the pole is 10m and the maximum distance is 16m.
Note:
A plane mirror produces a virtual, upright and same sized image of an object. The image appears to be situated at equal distance from the mirror surface. As the object distance is increased, plane mirrors can produce equally distant images, even vertically. The angle of incidence can vary from 0∘to90∘.
