Question

A pole of 25 meters long stands on the top of a tower 225 meters high. If $\theta$ is the angle subtended by the pole at a point on the ground which is at a distance $2.25\;{\rm{km}}$ from the foot of the tower then $\tan \theta$ is equal to

Answer 1

Hint : To solve this question, we will draw the triangle from the given data. From the figure we will find the perpendicular and base of the triangle. The tangent of the triangle can be defined as the ratio of the perpendicular and the base of the triangle. So, we will substitute the values of perpendicular and base in the expression of $\tan$ to get our answer.

Complete step-by-step answer :
The following is the schematic diagram of the pole.

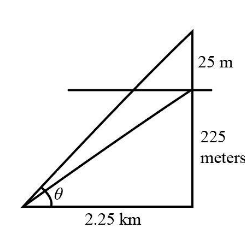
Given:
The height of the pole is $25\;{\rm{m}}$.
The height of the tower is $225\;{\rm{m}}$.
Also, it is given that the point on the ground is at a distance of $2.25\;{\rm{km}}$ from the foot of the tower.
Now, in the diagram we can see that $\theta$ is the angle subtended by the pole on a point on the ground.
We know that the basics of trigonometry formula,
$\tan \theta = \dfrac{P}{B}$
Where, $P$ is the perpendicular of the triangle and $B$ is the base of the triangle.
In our triangle perpendicular can be expressed as:
$\begin{array}{l} P = 25\;{\rm{m}} + 225\;{\rm{m}}\\\ P = 250\;{\rm{m}} \end{array}$
Also, base of the triangle can be expressed as:
$\begin{array}{l} B = 2.25\;{\rm{km}} \times \dfrac{{{\rm{1000}}\;{\rm{m}}}}{{{\rm{1}}\;{\rm{km}}}}\\\ B = 2250\;{\rm{m}} \end{array}$
Now we will substitute perpendicular and base in the expression of $\tan \theta$ , we get,
$\begin{array}{l} \tan \theta = \dfrac{{250\;{\rm{m}}}}{{2250\;{\rm{m}}}}\\\ \tan \theta = \dfrac{1}{9} \end{array}$
Hence, the value of $\tan \theta$ is $\dfrac{1}{9}$ .

Note : Make sure that the side opposite to the angle $\theta$ is the perpendicular of the triangle and the side at which angle is subtended is the base of the triangle. The general mistake that can happen in this problem is the confusion between the angle subtended by the tower and pole. But in our problem the angle asked is the angle subtended with the pole and not with the tower.