Solveeit Logo
Login

Question

Question: A pole is slightly inclined towards the east. At two points due west of it at distances \(a\,\,and\,...

A pole is slightly inclined towards the east. At two points due west of it at distances a  and  ba\,\,and\,\,b, the angle of elevation of the top of the pole are α  and  β\alpha \,\,and\,\,\beta respectively. The inclination of the pole to the horizon is:
A. tan⁡−1[a+bbcot⁡α−cot⁡β]{\tan ^{ - 1}}\left[ {\dfrac{{a + b}}{{b\cot \alpha - \cot \beta }}} \right]
B. tan⁡−1[b−abcot⁡α−acotβ]{\tan ^{ - 1}}\left[ {\dfrac{{b - a}}{{b\cot \alpha - acot\beta }}} \right]
C. cos⁡−1[a−bbcos⁡α−cos⁡β]{\cos ^{ - 1}}\left[ {\dfrac{{a - b}}{{b\cos \alpha - \cos \beta }}} \right]
D. sin⁡−1[a−bbcot⁡α−acot⁡β]{\sin ^{ - 1}}\left[ {\dfrac{{a - b}}{{b\cot \alpha - a\cot \beta }}} \right]

Explanation

Solution

Hint : Firstly, we will make a diagram according to the information in the question. Thereafter, we will solve and find the value of ccand hh, then find the inclined angle to get the answer.

Complete step-by-step answer :

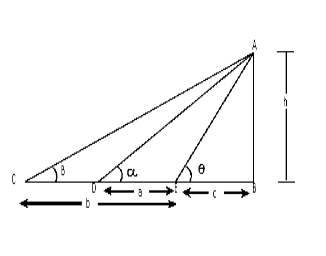
Let ABAB be a pole C  and  DC\,\,and\,\,D are the points from where it is observed.
Let AB=h,  BE=cAB = h,\,\,BE = c
Here, ED=a  and  EC=bED = a\,\,and\,\,EC = b
Now, inΔABD,  at  ∠B=90o\Delta ABD,\,\,at\,\,\angle B = {90^o}, by using trigonometric ratio, we have
tanα=ABBD tan⁡α=ABBE+ED  tan\alpha = \dfrac{{AB}}{{BD}} \\\ \tan \alpha = \dfrac{{AB}}{{BE + ED}} \\\
We will substitute the value of AB=h,  BE=cAB = h,\,\,BE = cand ED=a ED = a\,,we have
tan⁡α=ha+c\tan \alpha = \dfrac{h}{{a + c}}
(a+C)tan⁡α=h(a + C)\tan \alpha = h …..(i)
Similarly, in ΔABC,  at  ∠β=90O\Delta ABC,\,\,at\,\,\angle \beta = {90^{}}O, so by using trigonometric ratio we have
tanβ=ABBC tan⁡β=ABBE+EC  tan\beta = \dfrac{{AB}}{{BC}} \\\ \tan \beta = \dfrac{{AB}}{{BE + EC}} \\\
We will substitute the value of AB=h,  BE=cAB = h,\,\,BE = cand EC=bEC = b,we have
tan⁡β=hc+b\tan \beta = \dfrac{h}{{c + b}}
(b+c)tan⁡β=h(b + c)\tan \beta = h ……(ii)
Now, from equation (i) and (ii), we have
(a+c)tan⁡α=(b+c)tan⁡β(a + c)\tan \alpha = (b + c)\tan \beta
atan⁡α+ctan⁡α=btan⁡β+ctan⁡βa\tan \alpha + c\tan \alpha = b\tan \beta + c\tan \beta
atan⁡α−btan⁡β=ctan⁡β−ctan⁡αa\tan \alpha - b\tan \beta = c\tan \beta - c\tan \alpha
atan⁡α−btan⁡β=c(tan⁡β−tan⁡α)a\tan \alpha - b\tan \beta = c(\tan \beta - \tan \alpha )
⇒c=atan⁡α−btan⁡βtan⁡β−tan⁡α\Rightarrow c = \dfrac{{a\tan \alpha - b\tan \beta }}{{\tan \beta - \tan \alpha }} …….(iii)
Now, we will substitute the value of ccin equation (i), we have
h=atan⁡α+ctan⁡αh = a\tan \alpha + c\tan \alpha
h=atan⁡α1+tan⁡α(atan⁡α−btan⁡βtan⁡β−tan⁡α)h = \dfrac{{a\tan \alpha }}{1} + \tan \alpha \left( {\dfrac{{a\tan \alpha - b\tan \beta }}{{\tan \beta - \tan \alpha }}} \right)
Now, we will take LCM tan⁡β−tan⁡α,\tan \beta - \tan \alpha ,we have
h=atan⁡α(tan⁡β−tan⁡α)+tan⁡α(atan⁡α−btan⁡β)tan⁡β−tan⁡αh = \dfrac{{a\tan \alpha (\tan \beta - \tan \alpha ) + \tan \alpha (a\tan \alpha - b\tan \beta )}}{{\tan \beta - \tan \alpha }}
h=atan⁡αtan⁡β−atan⁡2α+atan⁡2α−btan⁡αtan⁡βtan⁡β−tan⁡αh = \dfrac{{a\tan \alpha \tan \beta - a{{\tan }^2}\alpha + a{{\tan }^2}\alpha - b\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}
h=atan⁡αtan⁡β−btan⁡αtan⁡βtan⁡β−tan⁡αh = \dfrac{{a\tan \alpha \tan \beta - b\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}
h=atan⁡αtan⁡β−btan⁡αtan⁡βtan⁡β−tan⁡αh = \dfrac{{a\tan \alpha \tan \beta - b\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}
Take tan⁡αtan⁡β\tan \alpha \tan \beta common in the numerator, we have
h=tan⁡αtan⁡β(a−b)tan⁡β−tan⁡αh = \dfrac{{\tan \alpha \tan \beta (a - b)}}{{\tan \beta - \tan \alpha }}
Now, in ΔABE\Delta ABE
tan⁡θ=ABBE\tan \theta = \dfrac{{AB}}{{BE}}
tan⁡θ=hc\tan \theta = \dfrac{h}{c} …..(iv)
Now, we will substitute ion value of hh and cc in equation (iv) , we have
tan⁡θ=(a−b)tan⁡αtan⁡β)tan⁡β−tan⁡αatan⁡α−btan⁡βtan⁡β−tan⁡α\tan \theta = \dfrac{{\dfrac{{(a - b)\tan \alpha \tan \beta )}}{{\tan \beta - \tan \alpha }}}}{{\dfrac{{a\tan \alpha - b\tan \beta }}{{\tan \beta - \tan \alpha }}}}
tan⁡θ=(a−b)tan⁡αtan⁡βtan⁡β−tan⁡α×tanβ−tan⁡αatan⁡α−btan⁡β\tan \theta = \dfrac{{(a - b)\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }} \times \dfrac{{tan\beta - \tan \alpha }}{{a\tan \alpha - b\tan \beta }}
tan⁡θ=(a−b)tan⁡αtan⁡β(atan⁡α−btainβ)\tan \theta = \dfrac{{(a - b)\tan \alpha \tan \beta }}{{(a\tan \alpha - btain\beta )}}
tan⁡θ=−(b−a)tan⁡αtan⁡β−(btan⁡β−atan⁡α)\tan \theta = \dfrac{{ - (b - a)\tan \alpha \tan \beta }}{{ - (b\tan \beta - a\tan \alpha )}}
tan⁡θ=(b−a)tan⁡αtan⁡βbtan⁡β−atan⁡α\tan \theta = \dfrac{{(b - a)\tan \alpha \tan \beta }}{{b\tan \beta - a\tan \alpha }}
Now, as we know that tan⁡θ=1cot⁡θ\tan \theta = \dfrac{1}{{\cot \theta }}
tan⁡θ=(b−a)1cot⁡α×1cot⁡β(bcot⁡β−acot⁡α)\tan \theta = \dfrac{{(b - a)\dfrac{1}{{\cot \alpha }} \times \dfrac{1}{{\cot \beta }}}}{{\left( {\dfrac{b}{{\cot \beta }} - \dfrac{a}{{\cot \alpha }}} \right)}}
⇒tan⁡θ=(b−a)1cot⁡α×1cot⁡β(bcot⁡α−acot⁡βcot⁡β×cot⁡α)\Rightarrow \tan \theta = \dfrac{{(b - a)\dfrac{1}{{\cot \alpha }} \times \dfrac{1}{{\cot \beta }}}}{{\left( {\dfrac{{b\cot \alpha - a\cot \beta }}{{\cot \beta \times \cot \alpha }}} \right)}}
⇒tan⁡θ=(b−a)1cot⁡α×1cot⁡β×cot⁡β×cot⁡αbcot⁡α−acot⁡β)\Rightarrow \tan \theta = \dfrac{{(b - a)\dfrac{1}{{\cot \alpha }} \times \dfrac{1}{{\cot \beta }} \times \cot \beta \times \cot \alpha }}{{b\cot \alpha - a\cot \beta )}}
⇒tan⁡θ=(b−a)bcot⁡α−acot⁡β\Rightarrow \tan \theta = \dfrac{{(b - a)}}{{b\cot \alpha - a\cot \beta }}
⇒θ=tan⁡−1(b−a)bcot⁡α−acot⁡β\Rightarrow \theta = {\tan ^{ - 1}}\dfrac{{(b - a)}}{{b\cot \alpha - a\cot \beta }}
So, the correct answer is “Option B”.

Note : Students remember that when you make an angle of elevation then follow this instruction it will help you. When you see an object above you, there is an angle of elevation between the horizontal and your line of sight to the object.