Question

A pole has to be erected at a point on the boundary of a circular park of diameter $13$m in such a way that the sum of its diameter from two diametrically opposite fixed gates A and B is $17$m. Is it possible to do so? If yes, at what distance from the two gates should the pole be erected?
A.$12$ from A and $5$ from B
B.Not possible
C.$13$ from A and $7$from B
D.$14$ from A and $6$from B

Answer 1

First, assume P be the pole and BP=x m then, AP=$17 - x$ m since AB is the diameter of the circular park. Then use Pythagoras theorem which is given as-
$\Rightarrow {H^2} = {P^2} + {B^2}$ where H=AB, P=BP and B=AP
Put the given values and form a quadratic equation. Solve the quadratic equation and find the value of x. Then we can find both BP and AP.

Complete step-by-step answer:
Let P be the pole and Gates A and B be diametrically opposite so AB=$13$ m as it is the diameter of the circular park.

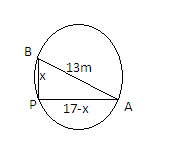
Also, the sum of two diametrically opposite fixed gates A and B is $17$m. So we can write-
AP+BP=$17$ m
Let BP=x m then, AP=$17 - x$ m
Now, since AB is diameter then the perpendicular drawn from the diameter on any point in the circle is the right angle in the semicircle. So $\angle APB = {90^\circ }$
Since from diagram it is clear that triangle APB is right angle triangle then by using Pythagoras theorem, we have-
$\Rightarrow {H^2} = {P^2} + {B^2}$
Here H=AB, P=BP and B=AP then, we have-
$\Rightarrow A{B^2} = B{P^2} + A{P^2}$
On putting the values of the given sides we get-
$\Rightarrow {13^2} = {x^2} + {\left( {17 - x} \right)^2}$
On using the formula${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$, we get-
$\Rightarrow {13^2} = {x^2} + {17^2} + {x^2} - 2 \times 17x$
On simplifying, we get-
$\Rightarrow 169 = 2{x^2} + 289 - 34x$
On further simplifying, we get-
$\Rightarrow 2{x^2} - 34x + 289 - 169 = 0$
On subtraction, we get-
$\Rightarrow 2{x^2} - 34x + 120 = 0$
On taking $2$ common and transferring, we get-
$\Rightarrow {x^2} - 17x + 60 = 0$-- (i)
This forms a quadratic equation. On factoring, we get-
$\Rightarrow {x^2} - 12x - 5x + 60 = 0$
On taking common terms out from the first two terms and last two terms we get-
$\Rightarrow x\left( {x - 12} \right) - 5\left( {x - 12} \right) = 0$
On simplifying, we get-
$\Rightarrow \left( {x - 5} \right) = 0$ or $\left( {x - 12} \right) = 0$
On solving we get-
$\Rightarrow x = 5$ or $x = 12$
Then either BP=$5$ m, AP=$17 - 5 =$ $12$m or BP=$12$ m, AP=$17 - 12 = 5$ m
Hence option A is the correct answer.
Note: Here the student may go wrong if they do not understand the language of the question and take the sum of the diametrically opposite gates AB to be $17$m and choose option B as it will be incorrect. Here the sum of the distances of the gates A and B from the pole is $17$m.