Question

A point $z$ moves on the curve $\left| {z - 4 - 3i} \right| = 2$ in an argand plane. The maximum and minimum value of $\left| z \right|$ is
A. 2, 1
B. 6, 5
C. 4, 3
D. 7, 3

Answer 1

The concept of complex numbers and the argand plane will be used in this problem. The square root of -1 is an imaginary number called iota and represented by the letter $i$. Compare the equation with the $\left| {z - {z_0}} \right| = r$. After that find the absolute value of the center. Then substitute the value to get the maximum and minimum value.

Complete step-by-step solution:
An argand plane is a plane that represents these complex numbers in a graphical form, where the horizontal axis(X) represents the real part, and the vertical axis represents the imaginary part. The general equation of a circle in the argand plane is $\left| {z - {z_0}} \right| = r$, where ${z_0}$ is the center and $r$ is the radius.
We have been given the equation $\left| {z - 4 - 3i} \right| = 2$ in an argand plane. When we compare it with the general equation of a circle, we can see that,
$\Rightarrow {z_0} = 4 + 3i$
So, the coordinates of the center are $\left( {4,3} \right)$.
And $r = 2$
The radius of the circle is 2 units.

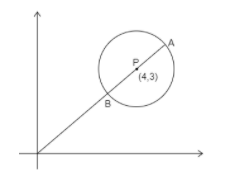
The point $z$ lies on the circumference of the imaginary circle. The value of $\left| z \right|$ will is maximum when it is extended along with line OP up to point A. Similarly, when we move in the opposite direction, the line OP cuts the circle at B, which will have the minimum value of $\left| z \right|$.
We know that the point P is represented by $4 + 3i$, so the magnitude of line OP can be calculated using the formula,
$\left| {a + ib} \right| = \sqrt {{a^2} + {b^2}}$
Substitute the values,
$\Rightarrow \left| {4 + 3i} \right| = \sqrt {{4^2} + {3^2}}$
Square the terms,
$\Rightarrow \left| {4 + 3i} \right| = \sqrt {16 + 9}$
Add the terms,
$\Rightarrow \left| {4 + 3i} \right| = \sqrt {25}$
Simplify the terms,
$\Rightarrow \left| {4 + 3i} \right| = 5$
The maximum value will be,
${\left| z \right|_{\max }} = OP + r$
Substitute the values,
$\Rightarrow {\left| z \right|_{\max }} = 5 + 2$
Add the terms,
$\Rightarrow {\left| z \right|_{\max }} = 7$
The minimum value will be,
${\left| z \right|_{\min }} = OP - r$
Substitute the values,
$\Rightarrow {\left| z \right|_{\min }} = 5 - 2$
Add the terms,
$\Rightarrow {\left| z \right|_{\min }} = 3$
Thus, the maximum and minimum value of $\left| z \right|$ is 7 and 3,

Hence, the option(D) is the correct answer.

Note: In such types of questions, identifying the equation and representing it graphically is the best method. If we did not know that the given equation is of an imaginary circle, the question would have become lengthy and calculative. So, we should remember the general equations of all conics and straight lines in the argand plane as well, as it helps in problem-solving. Also, we should keep in mind the various formulas related to the modulus of a complex number.