Question
Question: A point traversed 3/4th of the circle of radius R in time t. The magnitude of the average velocity o...
A point traversed 3/4th of the circle of radius R in time t. The magnitude of the average velocity of the particle in this time interval is :
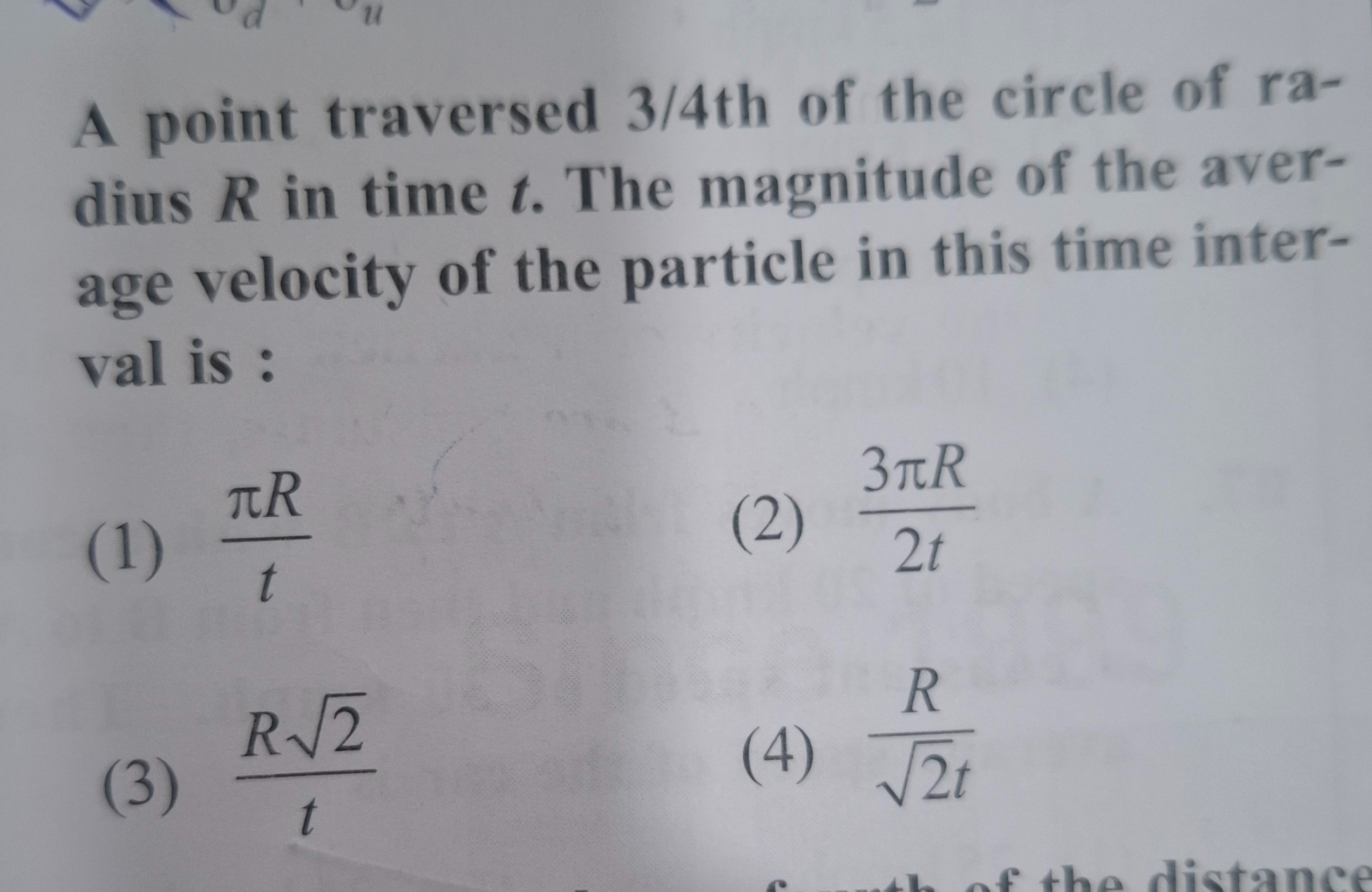
tπR
2t3πR
tR2
2tR
tR2
Solution
The problem asks for the magnitude of the average velocity of a particle that traverses 3/4th of a circle of radius R in time t.
-
Understanding Average Velocity:
Average velocity is defined as the total displacement divided by the total time taken.
vavg=ΔtΔr
The magnitude of the average velocity is ∣vavg∣=Δt∣Δr∣. -
Determining Displacement (Δr):
Let the circle be centered at the origin (0,0).
Assume the particle starts at point A on the positive x-axis, so its initial position vector is rA=Ri^.
The particle traverses 3/4th of the circle. This corresponds to an angular displacement of 43×2π=23π radians (or 270 degrees).
If the particle moves counter-clockwise from (R,0):
- After 90∘ (1/4 circle), it would be at (0,R).
- After 180∘ (1/2 circle), it would be at (−R,0).
- After 270∘ (3/4 circle), it would be at (0,−R).
So, the final position vector is rB=−Rj^.
The displacement vector Δr is the vector from the initial position to the final position:
Δr=rB−rA=(−Rj^)−(Ri^)=−Ri^−Rj^
The magnitude of the displacement ∣Δr∣ is the length of this vector:
∣Δr∣=(−R)2+(−R)2=R2+R2=2R2=R2
Alternatively, visualize the initial point (R,0) and the final point (0,−R). These two points form a right-angled isosceles triangle with the center of the circle (origin). The two equal sides are the radii R, and the displacement is the hypotenuse. By Pythagorean theorem, the length of the hypotenuse is R2+R2=2R2=R2.
-
Determining Time Taken (Δt):
The time taken is given as t. -
Calculating the Magnitude of Average Velocity:
Now, substitute the values into the formula for the magnitude of average velocity:
∣vavg∣=Δt∣Δr∣=tR2
