Question

A point source S is placed midway between two converging mirrors having equal focal length $f$ as shown in figure. Find the values of $d$ for which only one image is formed.

• A. d = $\sqrt{2}f$
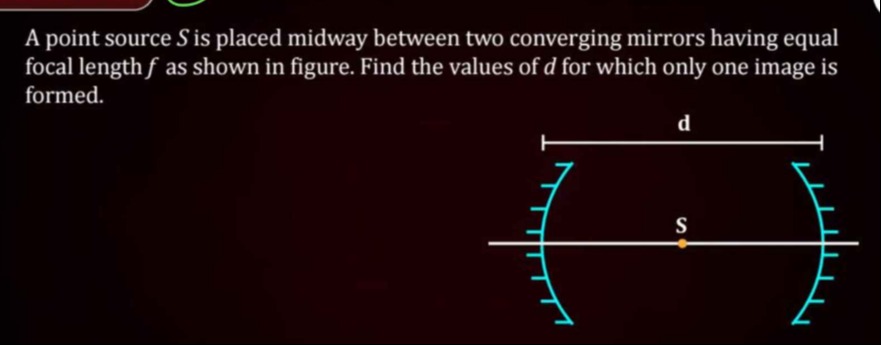
• B. d = $2f$
• C. d = $\frac{f}{2}$
• D. d = $f$

Answer 1

Answer: (A)

d = $\sqrt{2}f$

Answer 2

For a single image to be formed by two parallel mirrors, the system must behave as a single optical element. This occurs when the image formed by the first mirror is located at the focal point of the second mirror, and simultaneously, the image formed by the second mirror is located at the focal point of the first mirror.

Let Mirror 1 be on the left and Mirror 2 be on the right. The point source S is placed midway between them, so its distance from each mirror is $d/2$. The focal length of both mirrors is $f$.

Condition 1: The image formed by Mirror 1 is at the focal point of Mirror 2. The object distance for Mirror 1 is $u_1 = d/2$. Using the mirror formula $\frac{1}{v_1} - \frac{1}{u_1} = \frac{1}{f}$, we get: $\frac{1}{v_1} = \frac{1}{f} + \frac{1}{d/2} = \frac{1}{f} + \frac{2}{d} = \frac{d+2f}{fd}$ So, the image distance from Mirror 1 is $v_1 = \frac{fd}{d+2f}$.

The distance of this image from Mirror 2 is $u_2 = d - v_1$. For this image to be at the focal point of Mirror 2, its distance from Mirror 2 must be $f$. Thus, $u_2 = f$. $d - v_1 = f$ $d - \frac{fd}{d+2f} = f$ $\frac{d(d+2f) - fd}{d+2f} = f$ $\frac{d^2 + 2df - fd}{d+2f} = f$ $\frac{d^2 + df}{d+2f} = f$ $d^2 + df = f(d+2f)$ $d^2 + df = df + 2f^2$ $d^2 = 2f^2$ $d = \sqrt{2}f$ (Since $d$ must be positive, we take the positive root).

Condition 2: The image formed by Mirror 2 is at the focal point of Mirror 1. The object distance for Mirror 2 (considering the object S) is $u_2' = d/2$. The image distance from Mirror 2 is $v_2' = \frac{fd}{d+2f}$ (by symmetry). The distance of this image from Mirror 1 is $d - v_2'$. For this image to be at the focal point of Mirror 1, its distance from Mirror 1 must be $f$. Thus, $d - v_2' = f$. $d - \frac{fd}{d+2f} = f$ This is the same equation as derived for Condition 1, which leads to $d = \sqrt{2}f$.

Both conditions are met simultaneously when $d = \sqrt{2}f$.