Question

A point source $S$ is placed at the bottom of a transparent block of height $10mm$ and refractive index $2.72$ . It is immersed in a lower refractive index liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter $11.54mm$ on the top of the block. The refractive index of the liquid is,

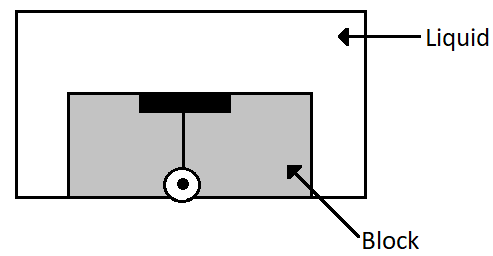
(A) $1.21$
(B) $1.30$
(C) $1.36$
(D) $1.42$

Answer 1

Hint The angle formed from the source to the bright spot will be the critical angle. This angle will be given by the tan of the angle which is the ratio of the height and the radius of the spot. From there we will get the sine of the angle. Using the value of the sine of the angle, we can find the refractive index of the liquid.

Formula Used: In this solution we will be using the following formula,
$\Rightarrow \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}}$
where ${n_1},{n_2}$ is the refractive index of the first and the second medium respectively and ${\theta _1},{\theta _2}$ are the angle of incidence and refraction respectively.

Complete step by step answer
To solve this problem, let us first draw the diagram of the source and the bright spot.

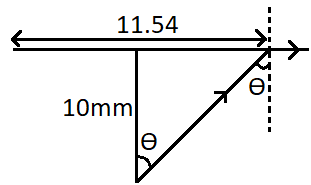
So the light from the source falls on the block to liquid interface at the critical angle. So the refracted ray becomes parallel to the surface. From the diagram, we take the radius of the bright spot as, $\dfrac{{11.54}}{2}mm$
that is, $5.77mm$ . The height of the block is given as, $10mm$ . According to the diagram, the tan of the angle will be,
$\Rightarrow \tan \theta = \dfrac{{5.77}}{{10}}$ . So we get the value as, $\tan \theta = 0.577$
On taking inverse on both the sides we get,
$\Rightarrow \theta = 30^\circ$
So the sine of this angle will be,
$\Rightarrow \sin 30^\circ = \dfrac{1}{2}$
Now, this angle is also the angle of incidence or the critical angle. Therefore the angle of refraction is $90^\circ$ . The first medium is the block having a refractive index of ${n_1} = 2.72$
Therefore, from Snell’s law, we have
$\Rightarrow \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}}$
So substituting the values we get
$\Rightarrow \dfrac{{{n_2}}}{{2.72}} = \dfrac{{\sin 30}}{{\sin 90}}$ .
The value of $\sin 90$ is 1. So taking $2.72$ to the RHS we get,
$\Rightarrow {n_2} = \dfrac{1}{2} \times 2.72$
On calculating we get
$\Rightarrow {n_2} = 1.36$
So the refractive index of the liquid is $1.36$
Therefore, the correct answer is option C.

Note
Snell's law is used to describe the relationship between the angle of incidence and the angle of refraction for a ray that is crossing the boundary between 2 different isotropic mediums. It states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction will be equal to the phase velocities in the two medium or reciprocal of the refractive indices of the two medium.