Question

A point source of power $P$ is projecting light in all direction. There is intensity $I_1$ observed at point $R$ and intensity $I_2$ on lens. Assuming paraxial ray approximation for lens then

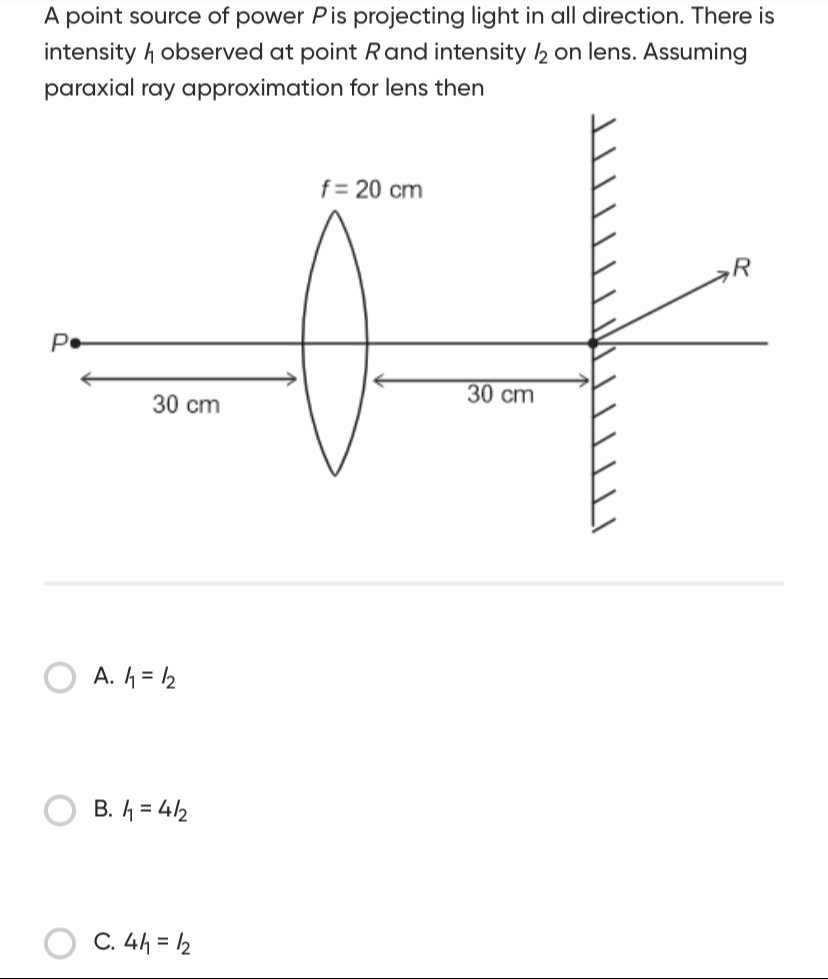
• A. $I_1 = I_2$
• B. $I_1 = 4I_2$
• C. $4I_1 = I_2$

Answer 1

Answer: (A)

A. $I_1 = I_2$

Answer 2

To solve this problem, we need to determine the location of the final image formed by the lens and the plane mirror, and then relate the intensities $I_1$ and $I_2$.

1. Intensity $I_2$ on the lens:
   The point source P emits light with power $P$ in all directions. The intensity $I_2$ at the lens is the power per unit area incident on the lens. The lens is at a distance $u_L = 30$ cm from the source P.
   The intensity of light from a point source at a distance $r$ is given by $I = \frac{P}{4\pi r^2}$.
   Therefore, the intensity of light incident on the lens is:
   $I_2 = \frac{P}{4\pi (30 \text{ cm})^2}$

2. Location of the final image:
   First, let's find the image formed by the lens.
   Object distance for the lens, $u = -30$ cm (using sign convention, object on the left).
   Focal length of the lens, $f = +20$ cm (for a convex lens).
   Using the lens formula:
   $\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
   $\frac{1}{v} - \frac{1}{(-30)} = \frac{1}{20}$
   $\frac{1}{v} + \frac{1}{30} = \frac{1}{20}$
   $\frac{1}{v} = \frac{1}{20} - \frac{1}{30} = \frac{3 - 2}{60} = \frac{1}{60}$
   So, $v = +60$ cm.
   This means the lens forms a real image, let's call it $I_L$, at a distance of 60 cm to the right of the lens.

Next, this image $I_L$ acts as an object for the plane mirror.
The mirror is placed at 30 cm to the right of the lens.
The image $I_L$ is at 60 cm to the right of the lens.
Therefore, the distance of $I_L$ from the mirror is $60 \text{ cm} - 30 \text{ cm} = 30 \text{ cm}$.
Since $I_L$ is to the right of the mirror, it acts as a virtual object for the plane mirror.
For a plane mirror, the image of a virtual object formed at a distance $x$ behind the mirror is a real image formed at a distance $x$ in front of the mirror.
So, the final image, let's call it $I_M$, will be formed at 30 cm to the left of the mirror.

Now, let's find the position of $I_M$ relative to the lens.
The mirror is 30 cm to the right of the lens.
The image $I_M$ is 30 cm to the left of the mirror.
So, the distance of $I_M$ from the lens is $30 \text{ cm (mirror to lens)} - 30 \text{ cm (image to mirror)} = 0 \text{ cm}$.
This means the final image $I_M$ is formed exactly at the location of the lens.

3. Intensity $I_1$ at point R:
   The problem states that intensity $I_1$ is observed at point R. The diagram shows R on the axis, and an arrow indicating light rays going towards R after reflection from the mirror. If R is the location of the final image, then R is at the lens.
   Let $A_{lens}$ be the area of the lens.
   The power collected by the lens from the source P is $\Phi_{inc} = I_2 \times A_{lens}$.
   Assuming no energy loss due to absorption or reflection by the lens or mirror, all this power $\Phi_{inc}$ will converge to form the final image $I_M$.
   Since the final image $I_M$ is formed at the lens itself (i.e., R is at the lens), the power $\Phi_{inc}$ converges at the lens.
   The intensity $I_1$ at point R (which is the lens) would be the power converging at the lens divided by the area of the lens:
   $I_1 = \frac{\Phi_{inc}}{A_{lens}}$
   Substitute $\Phi_{inc} = I_2 \times A_{lens}$:
   $I_1 = \frac{I_2 \times A_{lens}}{A_{lens}}$
   $I_1 = I_2$

Therefore, the intensity observed at point R ($I_1$) is equal to the intensity on the lens ($I_2$).