Question

A point source of light is placed ${\text{4 m}}$ below the surface of water of refractive index. The minimum diameter of a disc, which should be placed over the source, on the surface of water to cut-off all light coming out of water is
(1) $\,6{\text{ m}}$
(2) ${\text{3 m}}$
(3) ${\text{4 m}}$
(4) ${\text{2 m}}$

Answer 1

The point source emits rays of light in all directions so when these rays make an angle more than critical angle the perform total internal reflection so all the rays making angle less than critical angle form a disc shape of light coming out of surface of water, we need to use a disc to cut off these light rays from source.

Complete step by step answer:
When a point source is placed ${\text{4 m}}$ below the surface of water it emits light in all directions but all the rays do not pass through water surface due to total internal reflection which happens if the light ray makes an angle greater than or equal to critical angle C which is given by the formula
$\sin C = \dfrac{1}{\mu }$ , where $\mu$ is the refractive index of the surface of water.
All the rays coming out of the surface form a circular shape in which we will place a disc where it cuts off all the light and the disc will have its minimum diameter as the diameter of the circular shape formed.

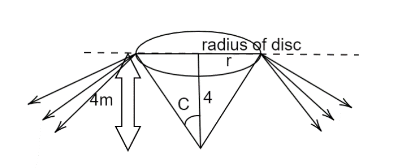
Now taking value of it given in question as $\dfrac{5}{3}$ we get $\sin C = \dfrac{1}{\mu } = \dfrac{1}{{\dfrac{5}{3}}} = \dfrac{3}{5}$ .
$\Rightarrow \tan C = \dfrac{3}{4}$ , now from the figure we can see a right-angled triangle where $r$ is the radius of the circular shape or the minimum radius of the disc.
$\tan C = \dfrac{r}{4} = \dfrac{3}{4} \Rightarrow r = 3{\text{ m}}$
Minimum diameter of disc $= {\text{d}} = 2r = 2\left( 3 \right) = 6{\text{ m}}$
Therefore the answer is option (1).

Note:
If the angle of incidence is bigger than the critical angle, the refracted ray will not emerge from the medium, but will be reflected back into the medium. This is called total internal reflection. The critical angle occurs when the angle of incidence where the angle of refraction is 90°.