Question

A point source of light is placed at the bottom of a water lake. If the area of the illuminated circle on the surface is equal to 3 times the square of the depth of the lake, the RI of water is:
A. $\sqrt {\pi + 1}$
B. $\sqrt {\dfrac{\pi }{3} + 1}$
C. $\dfrac{\pi }{3} + 1$
D. $\dfrac{\pi }{4} + 1$

Answer 1

Express the depth of the water lake in terms of radius of the illuminated circle using the given condition. Express the critical angle by referring to the diagram and then express the same using the formula for critical angle obtained using Snell’s law. Equate the two equations and find the refractive index of the water.

Formula used:
Critical angle, $\sin {\theta _C} = \dfrac{{{\mu _r}}}{{{\mu _i}}}$
Here, ${\mu _r}$ is the refractive index of the medium in which refracted ray is travelling and ${\mu _i}$ is the refractive index of the medium in which incident ray is travelling.

Complete step by step answer:
We assume the depth of the water lake is h and the radius of the illuminated circle is R.We know that the light from the source at the bottom can emerge from the water surface if the angle made by incident ray with normal equals the critical angle. We have given the condition; the area of the illuminated circle is 3 times the square of depth of the water lake. Therefore, we can write,
$\pi {R^2} = 3{h^2}$
$\Rightarrow {h^2} = \dfrac{{\pi {R^2}}}{3}$ …… (1)

We can draw the ray diagram of the given situation as follows,

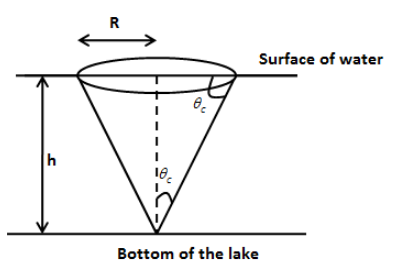
From the above figure, we can express $\sin {\theta _C}$ as follows,
$\sin {\theta _C} = \dfrac{R}{{\sqrt {{R^2} + {h^2}} }}$ …… (2)
We also know that, the sine of critical angle is the ratio of refractive index of the medium beyond the boundary to the refractive index of the medium through which the incident ray travels.
Therefore, $\sin {\theta _C} = \dfrac{{{\mu _a}}}{\mu }$
Here, $\mu$ is the refractive index of water and ${\mu _a}$ is the refractive index of air.

Since the refractive index of the air is 1, we can write,
$\sin {\theta _C} = \dfrac{1}{\mu }$ …… (3)
Equating equation (2) and (3), we get,
$\dfrac{1}{\mu } = \dfrac{R}{{\sqrt {{R^2} + {h^2}} }}$
Using equation (1) in the above equation, we get,
$\dfrac{1}{\mu } = \dfrac{R}{{\sqrt {{R^2} + \dfrac{{\pi {R^2}}}{3}} }}$
$\Rightarrow \dfrac{1}{\mu } = \dfrac{1}{{\sqrt {1 + \dfrac{\pi }{3}} }}$
$\Rightarrow \mu = \sqrt {1 + \dfrac{\pi }{3}}$

So, the correct answer is option B.

Note: To answer these questions, students should understand what is the critical angle? It is the angle of incident ray at which the refracted ray travels along the boundary between the two mediums. If the angle of incident is less than critical angle, the incident ray will not emerge from the surface of water.