Question

A point source of light is placed at a depth of $h=0.5\text{ m}$ below the surface of a fluid. $\left( \mu =\dfrac{5}{4} \right)$Then, the fraction of light energy that escapes directly from the fluid surface is:-
A.)0.1
B.)0.2
C.)0.3
D.)0.4

Answer 1

Hint: We know that light going from a denser to rarer medium gets reflected back into the denser medium if the angle of incidence of light is greater than the critical angle. So, all the light rays, which makes an angle less than the critical angle, escape out of the fluid surface. The ratio of the area from which the light can escape out to the total area gives the fraction of light that can escape from the fluid surface.

Complete step by step answer:
We know that the total internal reflection of light takes place when it goes from a denser to a rarer medium, and the angle of incidence made by the light with the medium boundary is greater than the critical angle. At the critical angle, the light ray grazes the medium boundary surface, as shown in the figure below.

So, when a point source of light is placed in a fluid at a depth of $0.5\text{ m}$, the light rays coming from the point source will hit the medium interface between the fluid and air. If the angle of incidence at this interface or boundary is less than the critical angle of the medium, then the light escapes from fluid to air. So, some light energy is lost in this way. If the angle of incidence is greater than the critical angle, the light at the boundary is reflected back into the fluid. The energy associated with the light remains in the fluid system.

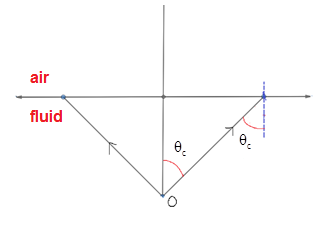
From the figure given above, the angle ${{\text{ }\\!\\!\theta\\!\\!\text{ }}_{\text{c}}}$ is the critical angle which is also equal to the angle subtended at O. So, the critical angle of a medium is given by the formula,
${{\theta }_{c}}={{\sin }^{-1}}\left( \dfrac{1}{\mu } \right)$
$\Rightarrow \sin {{\theta }_{c}}=\dfrac{1}{\mu }$ … equation (1)
In order to calculate the amount of light energy that is being lost, we need to calculate the solid angle made by the light ray at the boundary of the fluid-air surface. The ratio of the solid angle subtended at the boundary to the total solid angle of a sphere gives the ratio of light energy lost from the system.

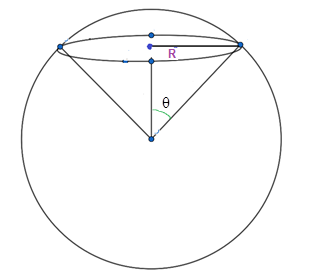
We can consider the interface as a part of a sphere of radius R. So, the solid angle subtended by a solid cone with an apex angle of $\text{2 }\\!\\!\theta\\!\\!\text{ }$ is given by the formula,
$\Omega =2\pi \left( 1-\cos {{\theta }_{c}} \right)$
From the relation in equation (1), we can write $\cos {{\theta }_{c}}=\sqrt{1-{{\left( \dfrac{1}{\mu } \right)}^{2}}}$. So, the above equation can be written as,
$\Omega =2\pi \left( 1-\sqrt{1-{{\left( \dfrac{1}{\mu } \right)}^{2}}} \right)$ … equation (2)
So the fraction of light energy lost can be expressed as the ratio of the solid angle subtended by the boundary to the solid angle subtended by a sphere.
$\text{Energy Lost}=\dfrac{\text{Solid angle subtended by the boundary}}{\text{Solid angle of a full sphere}}$
Substituting equation (2) in the above equation, we get,
$\text{Energy lost}=\dfrac{2\pi \left( 1-\sqrt{1-{{\left( \dfrac{1}{\mu } \right)}^{2}}} \right)}{4\pi }$
$\text{Energy lost}=\dfrac{2\pi \left( 1-\sqrt{1-{{\left( \dfrac{4}{5} \right)}^{2}}} \right)}{4\pi }$
$\therefore \text{Fraction of energy lost}=0.2$
So the answer to the question is the option (B).

Note:
Solid angle is a 2D angle in a 3D space. It is a dimensionless quantity whose unit is Steradian (sr). The solid angles are considered to be a part of a sphere. The solid angle subtended by a sphere is $4\pi$.
Solid angle is extensively used in numerous mathematical derivations in physics, from calculating the electric and magnetic field strength around charge distributions, to find the luminosity of various bodies and many more.
Total internal reflection is a consequence of refraction light at the boundaries of two optical mediums. According to the theory of refraction, light bends away from the normal when it travels from a denser medium to rarer medium, light bends towards the normal when it travels from a rarer to denser medium.