Question

A point source of light B is placed at a distance L in front of the center of a mirror of width(d) hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown in fig. The greatest distance over which he can see the image of the light source in the mirror is:

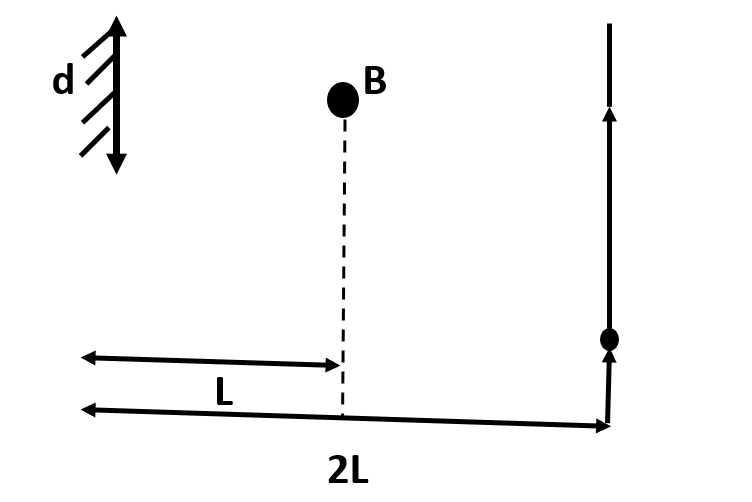
$\begin{aligned} & (a)\dfrac{d}{2} \\\ & (b)d \\\ & (c)2d \\\ & (d)3d \\\ \end{aligned}$

Answer 1

As the man moves towards the mirror, the greatest distance over which he can see the light source, will be determined by the fact that the first light ray that he sees and the last light ray he sees bouncing off the surface of the mirror . This area is the field of view for the person.

Complete step-by-step answer:
Let us further analyze the problem with the help of the following diagram:

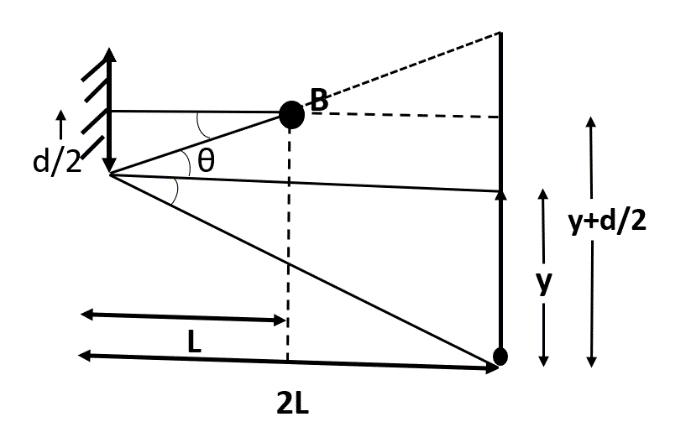
Here, we can clearly see the first light ray he can see. As the point source is symmetrically located at a distance $(\dfrac{d}{2})$ , therefore the field of view above the source of light and the field of view below the source of light will be same.
Hence if we calculate one, the greatest distance over which he can see the image of the light source will be double its value.
So, as per the diagram, in the smaller triangle:
$\Rightarrow \tan \theta =\dfrac{{}^{d}/{}_{2}}{L}$
$\Rightarrow \tan \theta =\dfrac{d}{2L}$ [Let this be equation number (1)]
In the bigger triangle, let the distance of the plane of incidence from the base be $(y)$, then using angle of incident is equal to angle of reflection, we get the angle as $\theta$ for the larger triangle as well. Then:
$\Rightarrow \tan \theta =\dfrac{y}{2L}$ [Let this be equation number (2)]
Equating the terms of equation number (1) and (2), we get:
$\begin{aligned} & \Rightarrow \dfrac{d}{2L}=\dfrac{y}{2L} \\\ & \Rightarrow d=y \\\ \end{aligned}$
Thus, the greatest visible distance below is equal to:
$\begin{aligned} & =\dfrac{d}{2}+y \\\ & =\dfrac{d}{2}+d \\\ & =\dfrac{3d}{2} \\\ \end{aligned}$
And this is also the greatest visible distance above.
Therefore, the greatest distance over which he can see the image of the light source is equal to:
$\begin{aligned} & =\dfrac{3d}{2}+\dfrac{3d}{2} \\\ & =3d \\\ \end{aligned}$
Hence, the greatest distance over which he can see the image of the light source is equal to$3d$ .

So, the correct answer is “Option D”.

Note: If the man walks further towards the mirror, then the reflected beam of light will just not be received by him and his field of view will start to decrease again. Thus, we can say that if he starts from very far away, his field of view increases till it reaches its maximum value and then starts to decrease once again.