Question
Question: A point source of light B is placed at a distance \(L\) in front of the center of a mirror of width ...
A point source of light B is placed at a distance L in front of the center of a mirror of width d, hung vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 2L from it as shown in the figure. The greatest distance over which he can see the image of the light source in the mirror is:
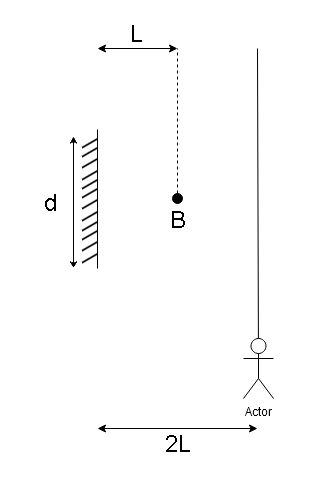
A.) 2d
B.) d
C.) 2d
D.) 3d
Solution
You can start by explaining what the distance of the image will be from the mirror. Then draw a well labelled diagram of the given situation, including the distance over which the man can see the source of light B in the mirror. Then use similarity between two triangles to find out half the distance over which the man can see the point source of light in the mirror. Then multiply it by two to get the result.
Complete step by step answer:
The distance of the image from the plane mirror is the same as the distance of the object from the mirror.
So, in this case the image of the point source of light B will be at a distance L from the mirror.
For the person to see the source of light B, a ray of light emerging from the point source of light B has to reach the man after striking the plane mirror.
The diagram given in the problem can be redrawn as follows
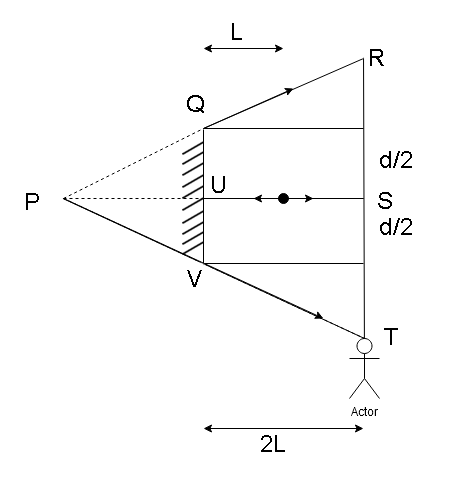
∵∠QPU=∠RPS
And ∠QUP=∠RSP=90∘
Thus, ΔPQU and ΔPRSare similar
∴PSPU=RSQU
2L+LL=RS2d
31=2(RS)d
RS=23d.
Thus, the man can see the point of source of light B in the mirror at a distance 23d above and below point S. Thus the man can see the point of source of light B in the mirror for a total distance of 23d+23d=3d .
Hence, the correct answer is option D.
Note:
Plane mirror is essentially a rectangular glass slab with a really smooth surface and is coated on one side by silver. Plane mirrors always produce an upright, virtual image. The size of the image is the same size as the object. The distance of the image from the plane mirror is the same as the distance of the object from the mirror.
