Question

A point source is situated at a distance $(x)$ which is less than $(f)$ from the pole of the concave mirror of focal length $f$. At time, $t=0$ , the point source starts moving away from the mirror with a constant velocity. Which of the graphs below represents best, variation of image distance $\left| v \right|$ with the distance $x$ between the pole of the mirror and the source.
(a)

(b)

(c)

(d)

Answer 1

We shall use the mirror formula first to write all the terms in relation with one another. Then, using these relations we vary our initial object distance from the concave mirror to determine the nature of the graph at certain specific points where we can determine the values of unknown parameters like the distance of image from the mirror in terms of focus and the object distance.

Complete answer:
Given, we have a concave mirror whose focus is $f$ .
The distance at which the object is kept is said to be $x$ . And,
The distance at which the image will form is said to be $v$ .
Now, it has also been strictly mentioned that we have to work under the assumption that the distance of the point source is less than the focus of the mirror.
Now, we have the mirror formula as follows:
$\Rightarrow \dfrac{1}{f}=\dfrac{1}{v}+\dfrac{1}{x}$
Now, using the mirror formula for:
Case (1): When distance of the point source tends to the focus, that is:
$\Rightarrow x\to f$
The distance at which the image is formed tends to be infinity.
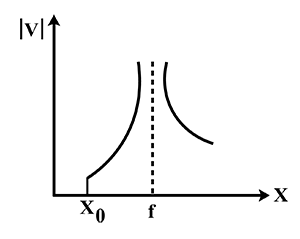
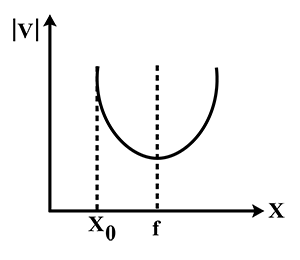
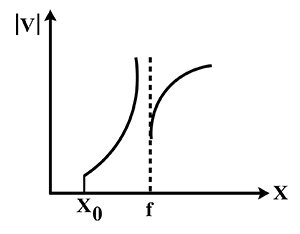
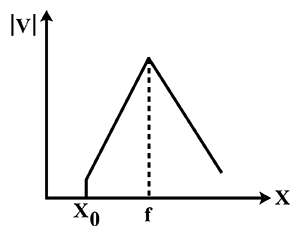
This criteria can be seen in the first and third graph. This means that option (b) and option (d) are incorrect.
Case (2): When the object is taken very far away from the mirror, that is when:
$\Rightarrow x\to \infty$
The distance at which the image is formed tends to be equal to $f$ .
This criteria is satisfied by the first graph only.
Thus, the first graph is the required plot of $\left| v \right|$ vs $(x)$ maintaining the condition $f < x$ .

Hence, option (a) is the correct option.

Note:
In these types of problems, we don’t need a specific set of data to plot the graph. We just need to have an idea of how the graph will turn out to be. And this can be done by putting some trivial values in the equation like zero, infinity or the length of focus, etc.