Question

A point source has been placed as shown in figure. What is the length on the screen that will receive reflected light from the mirror?

A) 2H
B) 3H
C) H
D) None

Answer 1

A point source is to be reflected along the mirror. The reflected ray will be obtained on the screen. With the help of triangles and equal angles, we can find the length of the screen, which will receive the reflected light.

Complete answer:
As we know that, a point source has been placed H distance from a perpendicular plane along which a mirror has been placed vertically H distance from the point source (E).
Firstly, we obtain the path of incident light and reflected light. In the figure, we see that when light rays EA and EG from point E are incident on the mirror AG, it is reflected on the screen at point C and D respectively.

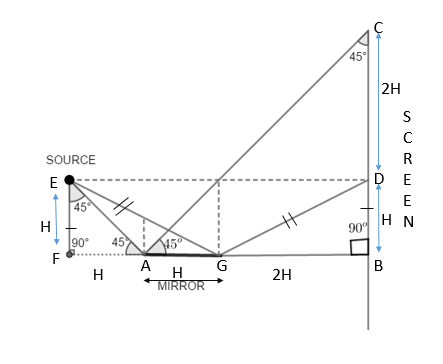
As EF and FA are both equal to H distance and $\angle \text{EFA}={{90}^{\text{o}}}$, so $\angle \text{FEA}=\angle \text{EAF}={{45}^{\text{o}}}$
Now, $\angle \text{EAC}={{90}^{\text{o}}}$, so $\angle \text{CAB}={{45}^{\text{o}}}$
In $\Delta \text{CAB}$, $\angle \text{CBA}={{90}^{\text{o}}}$ and $\angle \text{CAB}={{45}^{\text{o}}}$, so $\angle \text{BCA}={{45}^{\text{o}}}$.
Therefore, $\Delta \text{CAB}$ is isosceles. As AB = 3H so, $\text{AB}=\text{BC}=3\text{H}$
From the figure, point D is formed directly opposite to E, on the screen, at H distance from B.
Therefore,

& \text{BC}=\text{CD + DB }=\text{ }3\text{H} \\\ & \text{CD}=\text{2H} \\\ \end{aligned}$$ **Therefore, option A is the correct option.** **Note:** While drawing the diagram, we should be careful with the scaling. Try taking H = 2 cm, then 2H = 4 cm. Then the screen will be horizontally 4H = 8 cm from the source, and the screen will be 3H = 6 cm in height. Then the incident and reflected light ray will be at the appropriate angle.