Question

A point source causes a photoelectric effect from a small metal plate. Which of the curves in the figure may represent the saturation photocurrent as a function of the distance between the source and the metal?

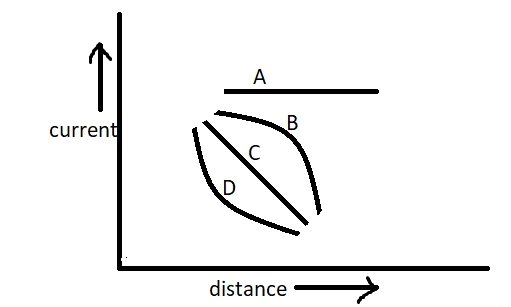
I. A
II. B
III. C
IV. D

Answer 1

We are already provided with the graphs distance-current . We just need a relation between intensity and distance to identify the current graph.

Formula used: We need to establish a proportionality relation;
Using De- Broglie hypothesis
${\text{I}} \propto \dfrac{{\text{1}}}{{{{\text{r}}^{\text{2}}}}}$
Here, ${\text{I}}$ is the intensity,
${\text{r}}$ is distance.

Complete step by step answer:
We already know that saturation current is the maximum current possible. It will be directly proportional to the number of electrons falling on the collector plate per second, which depends on the number of photons incident on the cathode as one photon contributes to one electron.
So, ${\text{I}} \propto \dfrac{{\text{1}}}{{{{\text{r}}^{\text{2}}}}}$
Therefore, the correct graph will be decreasing with power 2 of distance and it will be rapidly decreasing.
So, we need to see from the above options and select the approximate value.
Thus, the correct answer is option IV.

Additional Information:
The intensity or brightness of light as a function of the distance from the light source follows an inverse square relationship. The decrease goes as r squared because the area over which the light is spread is proportional to the distance squared. The energy carried in a wave depends on the wave's amplitude and its velocity. Again, as they spread, the energy carried is also spread, so as the distance from the source is increased, the amplitude is decreased, but this time as the square of the distance.

Note: It should be kept in mind that as the distance changes, the intensity changes by a factor of one divided by the square of the distance. Thus, doubling the distance decreases the light intensity to one-fourth of the original value.