Question

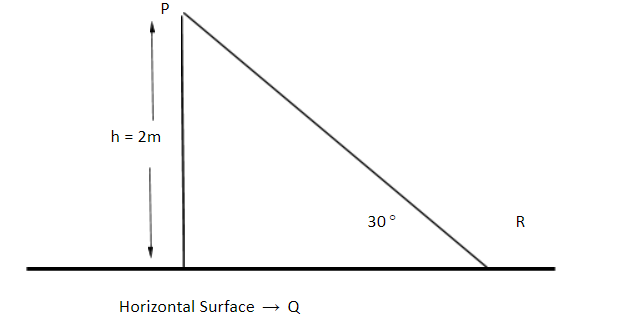
A point particle of mass m, moves along the uniformly rough QPR as shown in the figure. The coefficient of friction, between the particle and rough track equals μ. The particle is released, from rest, from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR o the track are equal to each other and no energy is lost when the particle changes direction from PQ to QR. The value of the coefficient of friction μ and the distance x (=QR) are respectively close to

A) 0.2 and 6.5 meter
B) 0.2 and 3.5 meter
C) 0.29 and 3.5 meter
D) 0.29 and 6.5 meter

Answer 1

The force between two surfaces such as sliding, or trying to slide, across each other is called friction. Friction is a non-conservative force that always opposes the motion of the body over the other. The movement of the object is always opposite to the friction of the direction of the object.

Complete step by step answer:
Let us first write the information given in the question.
The coefficient of friction = μ, the energy lost by the ball between PQ and QR is equal.
We have to find the value of the coefficient of friction μ and distance QR =x.
Here potential energy is dissipated due to frictional force.
Therefore, we can write the following.
Potential energy = work done by friction …………………….. (1)
Let us first calculate the work done from P to Q.
$\Rightarrow {\left( W \right)_{PQ}} = \mu mg(PQ\cos 30) = \mu mg2\sqrt 3$ ……………... (2)
Let us similarly calculate the work done from Q to R.
$\Rightarrow {\left( W \right)_{QR}} = \mu mg(QR) = \mu mgx$ …………………………….. (3)
The potential energy is given as below.
$PE=m g h$
Let us substitute the values.
$PE = 2mg$ …………………...(4)
Let us use the equation (1) and substitute the values from (2), (3), and (4).
$\Rightarrow 2mg= \mu mg \times$($x + 2\sqrt 3$)
Let us simplify it.
$\Rightarrow \mu = \dfrac{2}{{x + 2\sqrt 3 }}$ …………………………. (5)
Now let us use the condition given in question which says that energy dissipated in between PQ and QR is the same.
$\Rightarrow 2\sqrt 3 \mu mg = \mu mgx$
Let us solve it for x.
$\Rightarrow x = 2\sqrt 3 = 3.464m$ ……………………….. (6)
Let us now substitute the value of x in equation (5).
$\Rightarrow \mu = \dfrac{2}{{2\sqrt 3 + 2\sqrt 3 }} = \dfrac{1}{{2\sqrt 3 }} = 0.288$

Therefore, the correct option is (C).

Note:
The minimum angle of inclination of a plane with the horizontal at which an object placed on it just begins to slide is known as the angle of repose.
The coefficient of limiting friction is given as below.
$\mu = \tan {\theta _{angle - repose}}$