Question

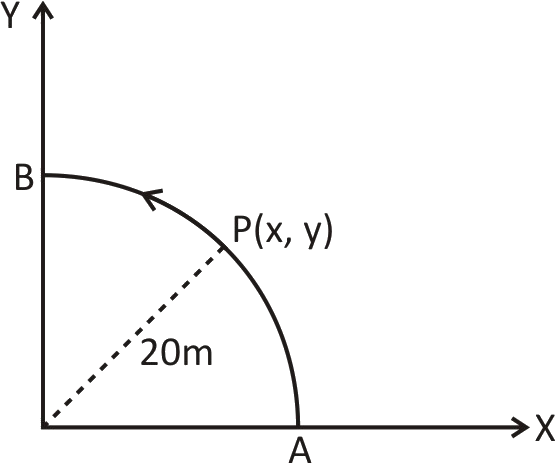
A point $P$ moves in counter-clockwise direction on a circular path as shown in the figure. The movement of $P$ is such that it sweeps out a length $s = {t^3} + 5$ , where $s$ is in metres and $t$ is in seconds. The radius of the path is $20\,{\text{m}}$. The acceleration of P when $t = 2\,{\text{s}}$ is nearly.

A. $13\,{\text{m}}{{\text{s}}^{ - 2}}$
B. $12\,{\text{m}}{{\text{s}}^{ - 2}}$
C. $7.2\,{\text{m}}{{\text{s}}^{ - 2}}$
D. $14\,{\text{m}}{{\text{s}}^{ - 2}}$

Answer 1

First of all, we will find out the velocity by differentiating the length with time along with its values time $t = 2\,{\text{s}}$. We will carry out the same for finding acceleration too. We will also calculate the centripetal acceleration. Lastly, we will find the net acceleration.

Complete step by step answer:
In the given question we are supplied the following data:
There is a point $P$ which moves in a counter clockwise direction on a circular path.
The movement of $P$ is the function of time, in which the length swept by it is given as $s = {t^3} + 5$.
Here $s$ is in metres and $t$ is in seconds.
The radius of the path is $20\,{\text{m}}$.
We are asked to find the acceleration of P when $t = 2\,{\text{s}}$.

To begin with, first of all we need to differentiate them with respect to time to get the expression of velocity. Then we will find the acceleration which is centripetal in nature.
So, let us proceed towards the solution:
Given distance is,
$s = {t^3} + 5$
We will differentiate with respect to time to get the velocity.
v\;=\; \dfrac{{ds}}{{dt}} \\\ \Rightarrow v = \dfrac{d}{{dt}}\left( {{t^3} + 5} \right) \\\ \Rightarrow v = 3{t^2} \\\

At time $t = 2\,{\text{s}}$ , the velocity can be found out as:
\Rightarrow v = 3{t^2} \\\ \Rightarrow v = 3 \times {2^2} \\\ \Rightarrow v = 12\,{\text{m}}{{\text{s}}^{ - 1}} \\\

As the science point $P$ is moving in a circular direction, so centripetal acceleration is associated with it.
So, the centripetal acceleration can be written as:
${a_{\text{c}}} = \dfrac{{{v^2}}}{R}$ …… (1)
Where,
${a_{\text{c}}}$ indicates centripetal acceleration.
$v$ indicates velocity.
$R$ indicates the radius of the path.

Now, by substituting the required values in the equation (1), we get:
{a_{\text{c}}} = \dfrac{{{{12}^2}}}{{20}} \\\ \Rightarrow {a_{\text{c}}} = 7.2\,{\text{m}}{{\text{s}}^{ - 2}} \\\

Again, we differentiate the velocity with respect to time and we get:
a = \dfrac{{dv}}{{dt}} \\\ \Rightarrow a = \dfrac{d}{{dt}}\left( {3{t^2}} \right) \\\ \Rightarrow a = 6t \\\

At time $t = 2\,{\text{s}}$ , the acceleration can be found out as:
{a_{\text{t}}} = 6t \\\ \Rightarrow {a_{\text{t}}} = 6 \times 2 \\\ \Rightarrow {a_{\text{t}}} = 12\,{\text{m}}{{\text{s}}^{ - 2}} \\\

Now, the net acceleration is given by:
a = \sqrt {a_{\text{t}}^2 + a_{\text{c}}^2} \\\
\Rightarrow a = \sqrt {{{12}^2} + {{7.2}^2}} \\\ \Rightarrow a = 13.99\,{\text{m}}{{\text{s}}^{ - 2}} \\\ \Rightarrow a \sim 14\,{\text{m}}{{\text{s}}^{ - 2}} \\\
Hence, the acceleration of P when $t = 2\,{\text{s}}$ is $14\,{\text{m}}{{\text{s}}^{ - 2}}$ .

Note:
While solving this problem, remember that fixed values of velocity and acceleration are not given as you have to find it out from the function provided in the question. First derivative of length with respect to time gives us velocity while the second derivative of length with respect to time gives acceleration. Translational acceleration and centripetal acceleration are two different things.