Question

A point $P\left( \sqrt{3},1 \right)$ moves on the circle ${{x}^{2}}+{{y}^{2}}=4$ . After covering a quarter of the circle, it leaves the circle tangentially. The equation of line along which the point moves after leaving the circle is
(a) $y=\sqrt{3}x+4$
(b) $\sqrt{3}y=x+4$
(c) $\sqrt{3}y=x-4$
(d) $y=\sqrt{3}x-4$

Answer 1

Hint : First, we will draw the circle as per given data. We will get as

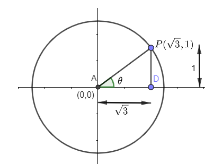
Then we will find angle $\theta$ using the formula $\tan \theta =\dfrac{opposite}{adjacent}$ . Then it is told that point moves to the quarter of the circle and leaves tangentially. So, it means that from point P till 90 degree we will mark point I in anticlockwise direction and in clockwise direction to point J. Then using the formula to find coordinate $\left( r\cos \theta ,r\sin \theta \right)$ we will get points I and J. Then, we will use equation to find tangent which is given as $x{{x}_{1}}+y{{y}_{1}}={{r}^{2}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ are coordinates at particular point. Thus, on solving for point I and J, we will get two options correct.

Complete step-by-step answer :
Then we will find angle $\theta$ using the formula $\tan \theta =\dfrac{opposite}{adjacent}$ . Then it is told that point moves to the quarter of the circle and leaves tangentially. So, it means that from point P till 90 degree we will mark point I in anticlockwise direction and in clockwise direction to point J. Then using the formula to find coordinate $\left( r\cos \theta ,r\sin \theta \right)$ we will get points I and J. Then, we will use equation to find tangent which is given as $x{{x}_{1}}+y{{y}_{1}}={{r}^{2}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ are coordinates at particular point. Thus, on solving for point I and J, we will get two options correct.

Here, first we will draw a circle and will plot the point $P\left( \sqrt{3},1 \right)$ approximately. We get as

Now, we will join the centre point with point P. So, we will get a triangle with some angle $\theta$ .

So, from this we get the value of angle using the trigonometric rule $\tan \theta =\dfrac{opposite}{adjacent}$ . By applying this rule, we get as
$\tan \theta =\dfrac{opposite}{adjacent}=\dfrac{PD}{AD}$
$\tan \theta =\dfrac{1}{\sqrt{3}}$
We know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$ . So, $\theta =30{}^\circ$ which in radian form can be written as $\theta =30{}^\circ \times \dfrac{\pi }{180{}^\circ }=\dfrac{\pi }{6}$ .
Now, it is given that the point covers the quarter circle and leaves the circle tangentially. It means that the circle has a total angle of 360. Quarter means $\dfrac{1}{4}$ so, we get an angle as $\dfrac{1}{4}\times 360=90{}^\circ$ . So, point moves $90{}^\circ$ in clockwise or anticlockwise direction. In radian form $90{}^\circ$ is $\dfrac{\pi }{2}$ . Figure is as shown below.

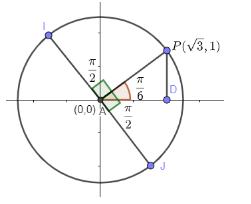
So, now total angle till point I from centre is $\dfrac{\pi }{6}+\dfrac{\pi }{2}=\dfrac{4\pi }{6}\Rightarrow \dfrac{2\pi }{3}$ and total angle from centre till point J is $\dfrac{\pi }{6}-\dfrac{\pi }{2}=\dfrac{-2\pi }{6}\Rightarrow -\dfrac{\pi }{3}$ .
So, coordinates of point I and J i.e. tangent can be found out using the formula $\left( r\cos \theta ,r\sin \theta \right)$ where the radius of the circle. So, we can find out from circle equation ${{x}^{2}}+{{y}^{2}}=4$ which is in form ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ . So, from this we will get $r=2$ .
Thus, coordinates of point I is $\left( 2\cos \dfrac{2\pi }{3},2\sin \dfrac{2\pi }{3} \right)$ and for J is $\left( 2\cos \dfrac{-\pi }{3},2\sin \dfrac{-\pi }{3} \right)$ .
Value of $\dfrac{2\pi }{3}=\pi -\dfrac{\pi }{3}$ . So, we can say that $\cos \dfrac{\pi }{3}=\dfrac{1}{2}$ and $\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}$ . As the tangent is in second quadrant, cos value will be negative and sin value will be positive.
Thus, on substituting the values and solving we get as $I\left( -1,\sqrt{3} \right)$ .
Similarly, for point J we get as $J\left( 1,-\sqrt{3} \right)$ .
Now, to find equation of tangent at a point formula will be $x{{x}_{1}}+y{{y}_{1}}={{r}^{2}}$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ are coordinates at particular point.
So, tangent t point I will be
$x\left( -1 \right)+y\left( \sqrt{3} \right)={{2}^{2}}$
$-x+\sqrt{3}y=4$
$\Rightarrow \sqrt{3}y=x+4$ …………………(1)
Similarly, for point J we get as
$x\left( 1 \right)+y\left( -\sqrt{3} \right)={{2}^{2}}$
$x-\sqrt{3}y=4$
$\Rightarrow x-4=\sqrt{3}y$ ………………………(2)
Thus, option (b) and (c) is correct.

Note : In this type of diagram figure is very necessary. If solved without a figure, there are chances of getting an incorrect answer. Students should know the formula to find coordinates points using the formula $\left( r\cos \theta ,r\sin \theta \right)$ . Also, students take radius of circle 4 instead of 2 and due to this silly mistake the whole answer will be wrong. So, be careful while solving it.