Question

A point P $\left( {\sqrt 3 ,1} \right)$ moves on the circle ${x^2} + {y^2} = 4$ and after covering a quarter of the circle leaves it tangentially. The equation of the line along which the point moves after leaving the circle is
$\left( 1 \right)y = \sqrt 3 x + 4$
$\left( 2 \right)\sqrt 3 y = x + 4$
$\left( 3 \right)y = \sqrt 3 x - 4$
$\left( 4 \right)\sqrt 3 y = x - 4$

Answer 1

Hint: In this question use the concept of slope between two points which is given as $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ and the general coordinates on the circle is given as $\left( {r\cos \theta ,r\sin \theta } \right)$ where $\theta$ is the angle between the line joining origin and that point and the x-axis either in clockwise direction or in anti-clockwise direction, later on in the solution use the concept that the general equation of tangent from any general point on the circle is given as $T = ax + by = {r^2}$ where (a, b) is the general point on the circle and r is the radius of the circle so use these concepts to reach the solution of the question.

Complete step-by-step answer:
reach the solution of the question.

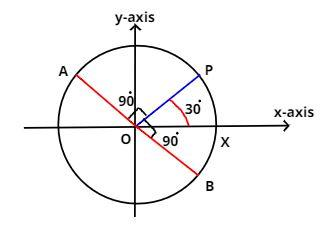
Given equation of circle is ${x^2} + {y^2} = 4$
So as we know the center of this circle is (0, 0) and radius is $\sqrt 4 = 2$ units.
Now it is given that the point P $\left( {\sqrt 3 ,1} \right)$ moves on the circle.
Now the both x and y coordinates of point P are positive so the point P lies on the first quadrant as shown in the figure.
Now the slope of point P and origin (0, 0) is given as
Let P = $\left( {\sqrt 3 ,1} \right)$ = (x1, y1) and origin (0, 0) = (x2, y2)
$\Rightarrow m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{0 - 1}}{{0 - \sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}$
Now as we know the slope is tan of $\theta$ w.r.t. positive x-axis.
$\Rightarrow \tan \theta = \dfrac{1}{{\sqrt 3 }} = \tan {30^0}$
$\Rightarrow \theta = {30^0}$
$\Rightarrow \angle POX = {30^0}$ as shown in figure.
Now it is given that point P moves quarter of the circle and leaves tangentially.
Therefore either point P goes clockwise or anti clockwise and reaches to A and B respectively.
So as we know that in a circle quarter of the circle rotation is 90 degree.
Therefore,
$\angle POA = \angle POB = {90^0}$
So the angle XOA = ${90^0} + {30^0} = {120^0}$
And the angle XOB = ${90^0} - {30^0} = {60^0}$
Let, ${\theta _1} = {120^0},{\theta _2} = {60^0}$
As ${\theta _2}$ is below the origin so it is written as ${\theta _2} = - {60^0}$
Now let the coordinates of A = $\left( {r\cos {\theta _1},r\sin {\theta _1}} \right)$ and the coordinates of B = $\left( {r\cos {\theta _2},r\sin {\theta _2}} \right)$, where r is the radius of the circle.
So the coordinates of A = $\left( {2\cos {{120}^0},2\sin {{120}^0}} \right) = \left( { - 1,\sqrt 3 } \right)$, $\left[ {\because \cos {{120}^0} = \dfrac{{ - 1}}{2},\sin {{120}^0} = \dfrac{{\sqrt 3 }}{2}} \right]$
And the coordinates of B = $\left( {2\cos \left( { - {{60}^0}} \right),2\sin \left( { - {{60}^0}} \right)} \right) = \left( {1, - \sqrt 3 } \right)$, $\left[ {\because \cos \left( { - {{60}^0}} \right) = \dfrac{1}{2},\sin \left( { - {{60}^0}} \right) = \dfrac{{ - \sqrt 3 }}{2}} \right]$
So the coordinates of A = $\left( { - 1,\sqrt 3 } \right)$ = (x3, y3),
And, B = $\left( {1, - \sqrt 3 } \right)$ = (x4, y4),
Now as we know that the equation of tangent on the circle through any general point (a, b) on the circle is given as
$T = ax + by = {r^2}$, where r is the radius of the circle.
So the tangent at point A is
$\Rightarrow {T_A} = x{x_3} + y{y_3} = {r^2}$
Now substitute the values we have,
$\Rightarrow {T_A} = - x + \sqrt 3 y = {2^2}$
$\Rightarrow {T_A} = - x + \sqrt 3 y = 4$
$\Rightarrow {T_A} = \sqrt 3 y = x + 4$
And the tangent at point B is
$\Rightarrow {T_B} = x{x_4} + y{y_4} = {r^2}$
Now substitute the values we have,
$\Rightarrow {T_B} = x - \sqrt 3 y = {2^2}$
$\Rightarrow {T_B} = x - \sqrt 3 y = 4$
$\Rightarrow {T_B} = \sqrt 3 y = x - 4$
So these are the required tangents.
Hence option (2) and (4) are correct.

Note – Whenever we face such types of questions the key concept involved in this question is the equation of tangent so always recall the equation of tangent which is stated above, then first calculate the slope of point P with the origin and moves point P by 90 degree in clockwise as well as in anti-clockwise as shown above (as the point P moves quarter of the circle) than calculate the angle of point A and B w.r.t. the positive x-axis then calculate the coordinates of point A and B as above then calculate the equation of the tangents as above which is the required answer.