Question

A point object of mass m is kept at (a,0) along x-axis. What mass should be kept at (-3a,0), so that center of mass lies at origin?

Answer 1

Given that a point object of mass m is kept at (a,0) along x-axis. Then using the equation of centre of mass equate that the centre of mass along the x-axis equal to zero. Then substitute the distance a, 3a and mass m in the equation of centre of mass we will get mass ${{m}_{1}}$such that the center of mass lies at origin.

Formula used:
The centre of mass is given by the equation,
${{x}_{CM}}=\sum\limits_{i}{\dfrac{{{m}_{i}}{{x}_{i}}}{M}}$
Where, M is the total mass of the system.
${{m}_{i}}$is the mass of an individual particle and ${{x}_{i}}$is the corresponding distance.

Complete step-by-step solution: -
A point object of mass m is kept at (a,0). Let the new mass be kept at (-3a,0) be ${{m}_{1}}$.

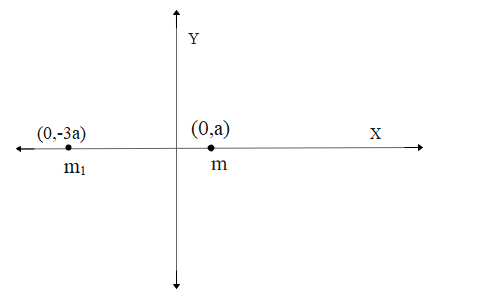
Then the centre of mass at origin is,
$\begin{aligned} & {{x}_{CM}}=0 \\\ & {{y}_{CM}}=0 \\\ \end{aligned}$
${{x}_{CM}}=0=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}}{{{m}_{1}}+{{m}_{2}}}$
${{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}=0$
$m\times a+{{m}_{1}}\times \left( -3a \right)=0$
$ma=3{{m}_{1}}a$
${{m}_{1}}=\dfrac{m}{3}$
Therefore to lie the center of mass lies at origin the mass $\dfrac{m}{3}$ should be kept at
(-3a,0).

Note: The centre of mass of a body can be defined as the point in which the whole mass of the body is concentrated. Thus for a system of particles this point where whole mass is concentrated is called the centre of mass. For calculation in mechanics which involve masses the concept of centre of mass is very useful. And also in orbital mechanics the point mass which is located in the centre of mass is used for forming the equations of motion.