Question

A point object O can move along vertical line AB as shown in the figure. When the image of the object is first visible to D then it is released at $t=0$ from rest from A. The time for which object will remain visible from D is –

& \text{A) }\sqrt{\dfrac{6L}{g}} \\\ & \text{B) }\sqrt{\dfrac{2L}{g}} \\\ & \text{C) }\sqrt{\dfrac{3L}{g}} \\\ & \text{D) t}\to \text{ }\infty \\\ \end{aligned}$$

Answer 1

We are given a system of plane mirror and an observer at a point between the object and the mirror. We need to find the relation that will help us understand the image formation and possibility of being observed at the given point.

Complete answer:
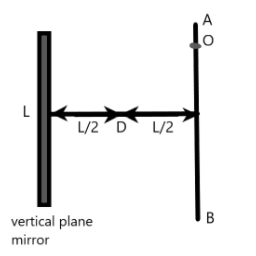
A vertical plane mirror of length L is kept in front of an observer at point D, which is at distance $\dfrac{L}{2}$ from the mirror and the plane of object. The object is moving along the line AB as shown in the figure.
It is given that at a point along AB starting from one end, the image of the object becomes visible to the observer at D. We need to find how long will the image be visible for the observer at point D.

We can see from the figure below that we can derive a few conclusions from the triangle properties. The angles opposite to the sides of a triangle are equal, for a right-angled triangle, the angle will be ${{45}^{0}}$. Also, the converse of this theorem is valid. We get the figure as per the conditions as shown below.

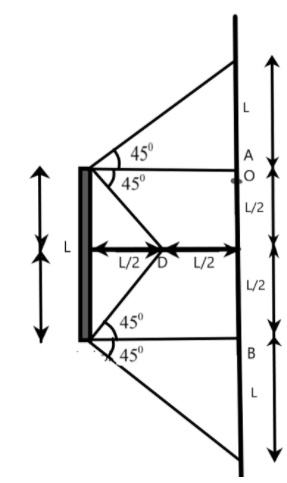
Now, we understand that the object will be visible at D between the area where the ray of reflection passes through the point D. The object can be viewed by the observer at D when it is in the length –

& {{L}_{eff}}=L+\dfrac{L}{2}+\dfrac{L}{2}+L \\\ & \Rightarrow {{L}_{eff}}=3L \\\ \end{aligned}$$ Now, we can use the equation of motion in one dimension to solve the time duration for the image being visible at D. $$\begin{aligned} & S=ut+\dfrac{1}{2}g{{t}^{2}} \\\ & \text{but, } \\\ & \text{initial velocity, }u=0 \\\ & \Rightarrow S=\dfrac{1}{2}g{{t}^{2}} \\\ & \Rightarrow t=\sqrt{\dfrac{2S}{g}} \\\ \end{aligned}$$ In our problem, the total distance is given as 3L, so we can compute the time duration as – $$\begin{aligned} & t=\sqrt{\dfrac{2S}{g}} \\\ & \Rightarrow t=\sqrt{\dfrac{2.3L}{g}} \\\ & \therefore t=\sqrt{\dfrac{6L}{g}} \\\ \end{aligned}$$ The time for which the object will be visible at the point D is $$\sqrt{\dfrac{6L}{g}}$$. **The correct answer is option A.** **Note:** We have used the triangle property in the whole solution. The sides of a triangle can be equal if the opposite angles of these sides are equal. The length of the sides should be considered carefully to avoid confusion between the two lengths.