Question

A point object is placed on the principal axis of a convex lens of focal length $f$ at a distance of $2f$ to the left of it. The diameter of the lens is $d$. An eye is placed at a distance of $3f$ to the right of the lens and a distance $h$ below the principal axis. The maximum value of $h$ to see the image is?
A. $d$
B. $d/2$
C. $d/3$
D. $d/4$

Answer 1

Principal axis of a lens is an imaginary horizontal line which passes through the optical centre of the lens. A convex lens is a converging lens which forms a real image (except when the object is placed between the optical centre and focus of the lens). Use this information and draw a ray diagram according to the question. You can use the lens formula to find the distance of image from the lens.

Formula Used:
Lens formula is given by $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ where $f$ is the focal length of the lens, $v$ is the image distance and $u$ is the object distance.

Complete step by step answer:
Let us first discuss the principal axis and image formation by convex lens. Principal axis of a lens is an imaginary horizontal line which passes through the optical centre of the lens. A convex lens is a converging lens which forms a real image (except when the object is placed between the optical centre and focus of the lens).
As given in the question that the object is at a distance of $2f$ to the left of the convex lens having diameter $d$. Let us find the image distance by using lens formula which is given by $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ where $f$ is the focal length of the lens, $v$ is the image distance and $u$ is the object distance.
The focal length of the convex lens is positive and $u = - 2f$ .
Substituting the values in the lens formula we have
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{{\left( { - 2f} \right)}}$
On simplifying we have
$\dfrac{1}{v} = \dfrac{1}{f} - \dfrac{1}{{2f}} = \dfrac{1}{{2f}}$
So, the distance of image $v = 2f$ .
As given in the question, an eye is placed at a distance of $3f$ to the right of the lens and a distance $h$ below the principal axis. So, we can plot the ray diagram which is given in the figure.

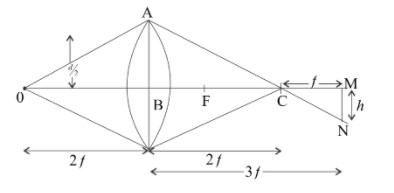
As from the ray diagram, $\Delta {\text{ABC}}$ is similar to the $\Delta {\text{MNC}}$
So, $\dfrac{{{\text{AB}}}}{{{\text{MN}}}} = \dfrac{{{\text{BC}}}}{{{\text{MC}}}}$
On substituting the values from the diagram we have
$\dfrac{{d/2}}{h} = \dfrac{{2f}}{f}$
On simplifying we have
$h = \dfrac{d}{4}$ which is the maximum value of $h$ to see the image.
Hence, option D is correct.

Note: You can also find the distance of image in this case without lens formula by using the fact that when an object is kept at centre of curvature of the lens then the image will always form at the centre of curvature of the lens on the opposite side. For a biconvex lens both the radius of curvatures is the same and equal to twice the focal length of the lens.