Question
Question: A point object is placed at a point Q in a glass slab as shown in the figure. The distance of the ob...
A point object is placed at a point Q in a glass slab as shown in the figure. The distance of the object as measured by an observer at P will be (μ = 1.5).
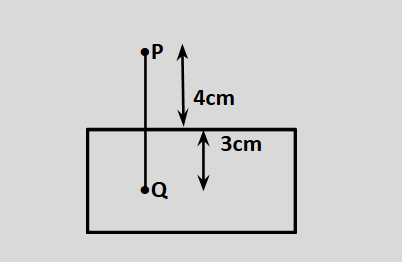
A. 7 cm
B. 6 cm
C. 5 cm
D. 7.5 cm
Solution
Hint: To calculate the distance measured by the object measured by an observer from point P we will use the formula: refractive index(μ) = Apparent depth(h)Real depth(H). Where Real depth is the distance object from the surface of a material medium while apparent depth is the distance of image formed due to refraction from the surface of the material medium.
Complete step by step answer:
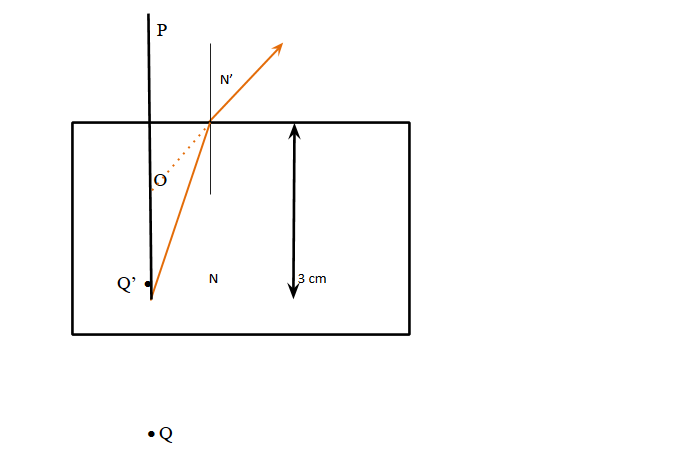
To find the required distance of the point P we have to draw a schematic diagram
which shows the image of point P formed by the refraction of light phenomenon.
The image of object Q is formed at Q’ by the phenomenon of refraction. So, from the diagram we can have the real depth is OQ and apparent depth is OQ’.
Now for calculating the apparent depth we use the formula :
refractive index(μ) = Apparent depth(h)Real depth(H)
We have given that:-
Real depth (OQ) = 3 cm and refractive index(μ) = 1.5
Now substituting the given value in the above expression. we get:
The image of point Q is formed at Q’. So, the observer at point P will see the apparent image at Q’.
Therefore, the required distance from point P is PQ’= PO + OQ’.
Hence, Option (B) is the correct answer.
Note: The formula used for solving this question came from one of the great applications of Snell’s law of refraction for the case of water and air media systems. It is one of the special cases of refraction when an object is placed in a material medium and the observer sees its image from the air medium. So for solving every system of a pair of media the same formula will not be valid. To tackle such kinds of conceptual questions one should have to derive the various formula for refraction phenomenon and also care about the condition for deriving them like:- the angle of incidence and the refraction is very small such that:- tanθ≈θ,sinθ≈θ and cosθ≈1 for very small θ.
