Question

A point object is placed at a distance of ${\text{12}}\,{\text{cm}}$on the axis of convex lens of focal length ${\text{10}}\,{\text{cm}}$. On the other side of the lens, a convex mirror is placed at a distance of ${\text{10}}\,{\text{cm}}$ from the lens such that the image formed by the combination coincides with the image itself. What is the focal length of the convex mirror?
A. ${\text{20}}\,{\text{cm}}$
B. ${\text{25}}\,{\text{cm}}$
C. ${\text{30}}\,{\text{cm}}$
D. ${\text{35}}\,{\text{cm}}$

Answer 1

First, draw a ray diagram using the given values; observe how the rays get refracted and reflection. Use lens formula to find the object distance. Recall the condition for which the rays trace back its path so the final image and object coincides. Use this condition to find the focal length of the convex mirror.

Complete step by step answer:
Given, object distance from the convex lens is $u = - 12\,{\text{cm}}$. Focal length of convex lens, $f = 10{\text{cm}}$. Distance between convex mirror and convex lens is $d = 10{\text{cm}}$
Now, we draw a ray diagram for the problem.

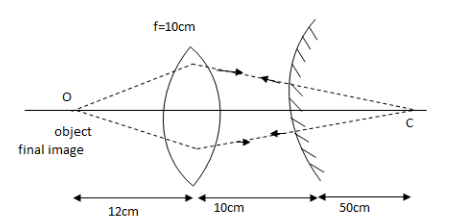
It is given that the image formed by the combination of convex lens and convex mirror coincides with the object. This means that the rays from the object are retracing its path after refraction and reflection from the lens and mirror respectively. For such a situation to happen, the image of a convex lens should form at the centre of curvature of the convex mirror.

Let us first find the image distance say $v$ for convex lens using lens formula which is,
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Putting the values of $u$ and $f$ we get

\Rightarrow v = \dfrac{{120}}{2} \\\ \Rightarrow v = 60\,{\text{cm}} $$ The image is formed at the centre of curvature of mirror and the mirror is at the distance of $$10{\text{cm}}$$ from the lens, so centre of curvature will be, $$R = v - d$$ Putting the values of $$v$$ and $$d$$ we get $$R = 60 - 10 \\\ \Rightarrow R = 50{\text{cm}} $$ Focal length of mirror is half of its radius of curvature, so focal length of the given convex lens will be, $$F = \dfrac{R}{2} = \dfrac{{50}}{2} = 25{\text{cm}}$$ **Hence, the correct option is B.** **Note:** : Remember the object distance is always taken as negative , this is because distances from the left side of the principal axis are taken as negative and distances from right side of principal axis are taken as positive. There are two important formulas to remember one is lens formula which we have used in the above question and the other is mirror formula which is $$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$$.