Question

A point object is placed at a distance of 30 cm from a convex mirror of focal length 30 cm. The image will form at
(A) Infinity
(B) Pole
(C) Focus
(D) 15 cm behind the mirror

Answer 1

To solve this question you should know what a convex mirror is and what a mirror is. With the general equation of the mirror equation, we can find where the image is formed with the given details in the question. Convex Mirror: A spherical mirror whose reflecting surface is curved outwards is called a convex mirror. Mirrors are good reflectors. A mirror can be made by silvering a metal surface with glass in front and paint at its back.

Complete step by step solution:

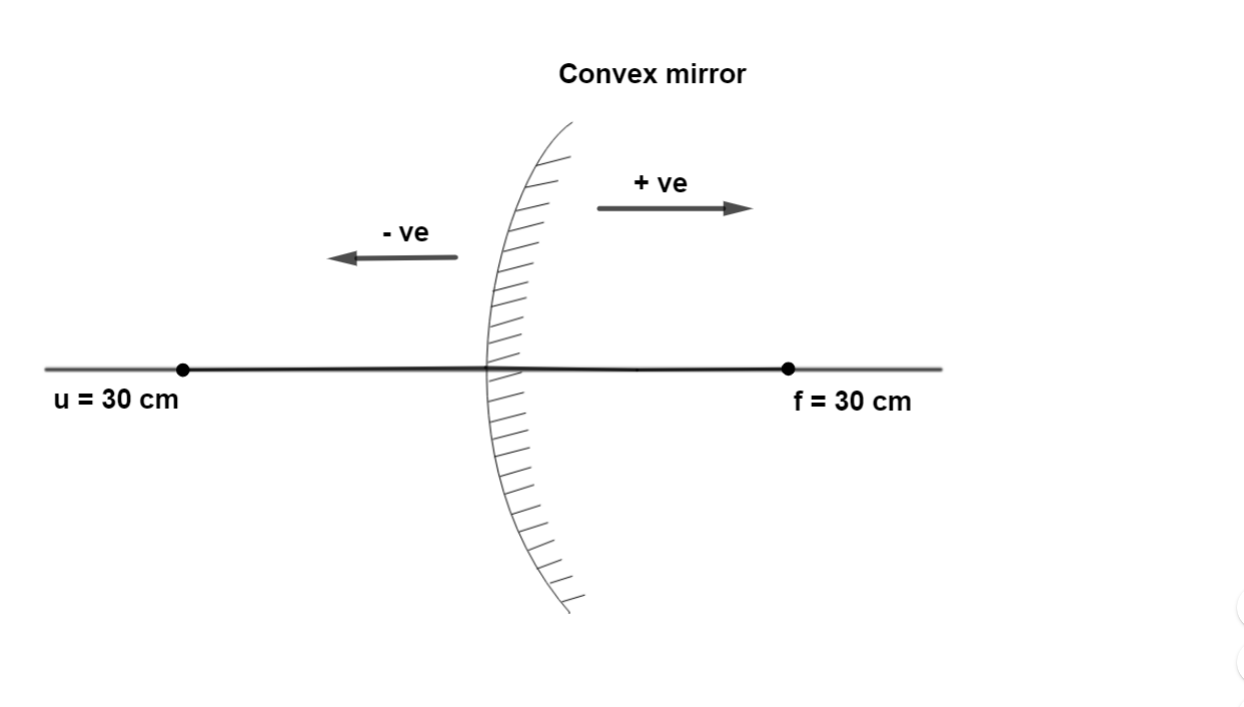
A point object is placed 30 cm from the convex mirror of focal length 30 cm.
Mirror formula: In a spherical mirror, there is a relation between object's distance u, image distance v and principal focus of the mirror f.
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Therefore, from the figure and given data
$u{\text{ = - 30 cm}}$
$f{\text{ = 30 cm}}$
Using the mirror formula,
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Substituting the values,
$\dfrac{1}{v} + \dfrac{1}{{ - 30}} = \dfrac{1}{{30}}$
Upon simplifying, we get
$\Rightarrow \dfrac{1}{v} = \dfrac{2}{{30}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{15}}$
$\therefore v{\text{ = 15 cm}}$

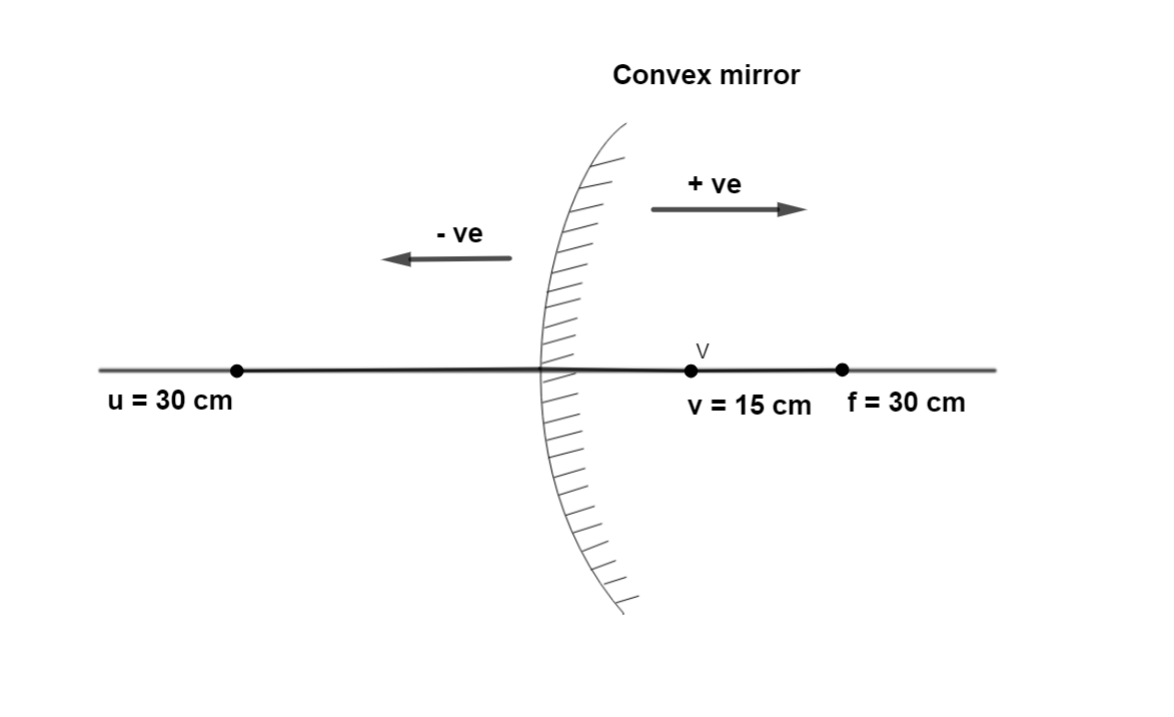
Therefore, the image is formed 15 cm behind the convex mirror.

So, the correct answer is option (D)

Additional information:
Concave Mirror: A spherical mirror, whose reflecting surface is curved inwards is called a concave mirror It means reflecting (polished) surface faces the center of the sphere from which it is made.
Magnification by Mirror: The extent by which a mirror extends or reduces the size of an image with respect to an object is called the magnification factor of a mirror. It is represented by m. If the size of an object is h and its image by a spherical mirror is h’. Then magnification factor of mirror is
$m{\text{ = - }}\dfrac{v}{u} = \dfrac{{h'}}{h}$

Note:
Convex mirrors are preferred over plane mirrors as rear-view mirrors because they give diminished images of objects and hence can cover a larger field of view. A convex mirror always produces a virtual image, because f is always greater than zero and u is less than zero so from the mirror formula the v will be always positive. Hence the image is always virtual.