Question

A point object is placed at a distance of 25 cm from a convex lens. Its focal length is 22 cm. A glass slab of refractive index 1.5 is inserted between the lens and the object, then the image is formed at infinity. Find the thickness of the glass slab (in cm).

Answer 1

Hint:
1. When an object is placed at the focus of a convex lens, its image is formed at infinity.
2. Shift due to glass slab:
$s = t(1 - \dfrac{1}{\mu })$ …… (1)
Where,
t is thickness of glass slab
$\mu$ is refractive index of glass

Complete step by step answer:

Given:
1. Distance of object from convex lens (u) = 25 cm.
2. Focal length of convex lens (f) = 22cm.
3. Refractive index of glass slab () = 1.5.
4. Distance of object from convex lens (u) = infinity.

To find: Thickness of glass slab (t) in cm.

Rough sketch:

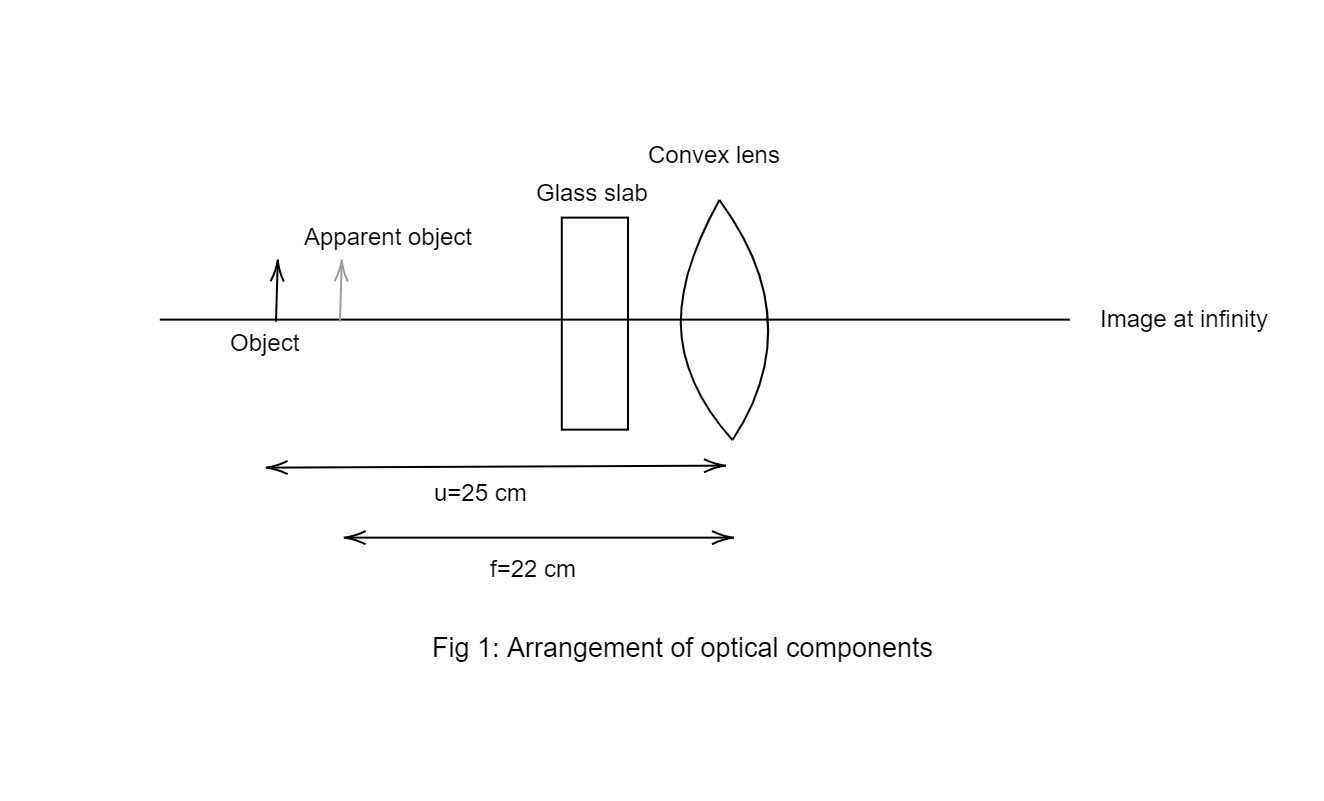
Step 1 of 3:
After inserting the glass slab, the image of the object is formed at infinity. This implies that after inserting the glass slab, the apparent distance of the object from the lens became equal to the focal length of the lens.

Step 2 of 3:
Find the value of s:
Shift due to glass slab $s = t\left(1 -\dfrac{1}{\mu } \right )$

$=\text u - \text f$
$=\left ( 25-22 \right )\text cm$
$=3cm$

Step 3 of 3:
Put the values of s and in eq(1):

$3= t\left ( 1-\dfrac{1}{1.5} \right )$
$t=\dfrac{3\times 1.5}{0.5}$
$t=9\text cm$

Additional Information:
Due to refraction from the glass slab, there is an apparent shift in the path of incident light. Hence, light emergent out of glass slab will be parallel to incident light but shifted. So, when glass slab is inserted the actual position of focus gets shifted closer to the lens.

Note: Parallel rays emerge from a convex lens, when object (source) is placed at the focus of the lens.