Question

A point object is placed at a distance $10{\text{ }}cm$ and its real image is formed at a distance of $20{\text{ }}cm$ from the concave mirror. If the object is moved by $0.1{\text{ }}cm$ towards the mirror, the image will shift by about
A) $0.4{\text{ }}cm$ away from the mirror.
B) $0.4{\text{ }}cm$ towards the mirror
C) $0.8{\text{ }}cm$ away from the mirror
D) $0.8{\text{ }}cm$ towards the mirror

Answer 1

We can use the mirror formula to find the focal length of the mirror as we have the distance of the object and distance of the image. After that, we can calculate the final distance of the image when the object shifts by $0.1{\text{ }}cm$. If there is any change in the final distance, then it will be the shift in the image's position.

Complete step by step answer:
According to the question, $MN$ is a concave mirror. $P$ is the pole of the mirror and $F$ is the focal length. $AB$ is the object at a distance $10cm$ and ${A^{'}}{B^{'}}$ is the image of $20cm$.

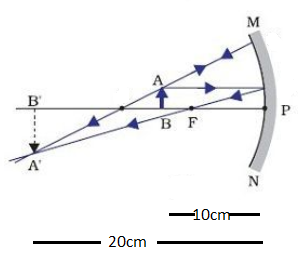
We have a concave mirror which has ${\text{u = initial distance = 20cm}}$ and ${\text{v = final distance = 10cm}}$.
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$,
Putting these values in the mirror formula, we get
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{{( - 20)}} + \dfrac{1}{{( - 10)}}$
On simplification,
$\Rightarrow f = \dfrac{{20}}{3}cm$
So, the focal length of the mirror is $\dfrac{{20}}{3}cm$.
Now, according to the question, when the object moves $0.1cm$ toward the mirror then $XY$ is the object at a distance $9.9cm$ and ${X^{'}}{Y^{'}}$ is the image.

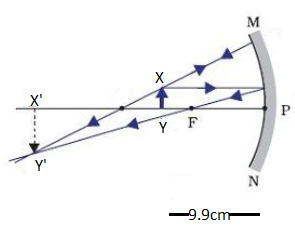
According to the question the object is moving towards the mirror $0.1cm$. So, the new value of $u = 10 - 0.1 = 9.9cm$
Again, using the mirror formula and putting $f = \dfrac{3}{{20}}cm$ and ${u_1} = 9.9cm$, we get-
$\dfrac{1}{f} = \dfrac{1}{{{u_1}}} + \dfrac{1}{{{v_1}}}$
$\Rightarrow \dfrac{1}{f} - \dfrac{1}{{{u_1}}} = \dfrac{1}{{{v_1}}}$
On substituting the corresponding values,
$\Rightarrow \dfrac{3}{{20}} - \dfrac{1}{{{{(9.9)}_1}}} = \dfrac{1}{{{v_1}}}$
On simplifications,
$\Rightarrow {v_1} = 20.4cm$

The final distance will become $20.4cm$.
So, The change in final distance $= 20.4 - 20 = 0.4{\text{ }}cm$

$\therefore$ The image will shift about $0.4{\text{ }}cm$ away the mirror as the change in final distance is positive. Therefore, option (A) is correct.

Note:
The initial distance and the final distance gives the focal length of the concave mirror when the object is not moved. The distance moved by the object is subtracted from the initial distance. The initial and final distances will be put with a negative sign in the mirror equation. The focal length of the mirror is the same for all objects and their images.