Question

A point mass m is connected at one end of an ideal spring (the other end of spring is fixed on a horizontal smooth surface). Complete arrangement is placed over a smooth horizontal plane. Horizontal velocity $v_0$ is given to point mass when spring is at its natural length $l_0$. Find the maximum elongation (approximately) in the spring. (Given $l_0=1\;m, v_0=1\;ms^{-1}, m=1\;kg, k=1\;Nm^{-1}$)

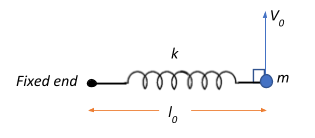
A. $0.839\;m$
B. $0.5\;m$
C. $1.2\;m$
D. $1.0\;m$

Answer 1

Obtain expressions for the initial and final angular momenta and energy for the system. Remember to account for the kinetic energy of the ball and the (kinetic) potential energy of the spring for the final energy. Use the laws of conservation of angular momentum and energy to arrive at equations that you can arithmetically solve after plugging in the given values to obtain a polynomial equation for the elongation, for which you can use a root plot to easily arrive at a real-valued solution.

Formula Used:
Conservation of angular momentum $L_i = L_f$
Law of conservation of energy $E_i = E_f$
Spring potential energy $P=\dfrac{1}{2}kx^2$

Complete Step-by-Step Solution:
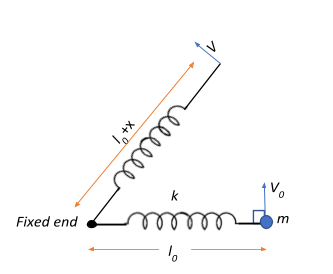
We have a point mass $m=1\;kg$ connected to a spring of natural length $l_0$ and spring constant $k=1\;Nm^{-1}$. The point mass is given a horizontal velocity of $v_0=1\;ms^{-1}$, which makes the point mass and the spring rotate about the fixed end. This means that the point mass and the spring execute an angular motion with respect to the fixed end.

Let the initial angular momentum of the system be $L_i = mv_0l_0$.

Now, let the spring reach a maximum elongation of x when the angular velocity is v. Then the length of the spring now becomes $(l_0+x)$.

The final angular momentum of the system will be $L_f = mv(l_0+x)$

Also, the initial energy of the system will just be the kinetic energy of the point mass, $E_i = \dfrac{1}{2}mv_0^2$.

The final energy of the system will be the sum of the kinetic energy of the point mass and the potential stored in the spring due to its elongation, $E_f = \dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2$

From the principle of conservation of angular momentum, we have that for an isolated system, the total initial angular momentum will be equal to the total final angular momentum of the system, i.e.,
$L_i = L_f$
$\Rightarrow mv_0l_0 = mv(l_0+x) \Rightarrow v_0l_0 = v(l_0+x)$

Substituting $v_0=1\;ms^{-1}$ and $l_0=1\;m$, we get:
$1=v(1+x) \Rightarrow v = \dfrac{1}{1+x}$

From the law of conservation of energy which says that, for an isolated system, the sum of all energies remains a constant, which means that the total initial energy will be equal to the total final energy of the system, i.e.,
$E_i = E_f$
$\Rightarrow \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2 \Rightarrow mv_0^2=mv^2+kx^2$

Plugging in $m=1\;kg$, $v_0=1\;ms^{-1}$and $k=1\;Nm^{-1}$ we get:
$1 = v^2 + x^2$

But we have $v = \dfrac{1}{1+x}$, which we plug in above:
$1 = \left(\dfrac{1}{1+x}\right)^2 + x^2$
$\Rightarrow (1+x)^2 = 1+ x^2(1+x)^2$
$\Rightarrow 1+x^2+2x = 1 + x^2+x^4+2x^3$
$\Rightarrow x^4+2x^3-2x=0$
$\Rightarrow x^3 + 2x^2 -2 =0 \Rightarrow x^2(x+2) -2=0$

Solving the above equation is a bit tedious which we will avoid doing here. Instead, we obtain a root plot for the above equation from which the intersection of the curve with the x-axis gives the real solution.

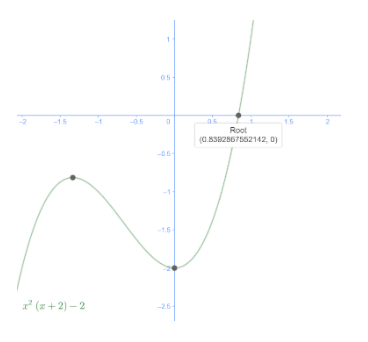
From the root plot we see that the real-value for the solution of x of the above equation lies at $x=0.8393$, which is indicative of the maximum elongation of the spring.

Therefore, the correct choice would be A. $0.839\;m$.

Note:
It is important to understand the distinction between natural length and equilibrium length of the spring since these terms may be mistakenly interchangeably used. The natural length of the spring is the length of the spring when it is not under any kind of tensional elongation or compression. However, the equilibrium length of the spring is the length when the spring is under the influence of a load.

Note that in the above problem, since the system was in the horizontal plane where the entire setup was placed on the horizontal surface, though the spring was connected to a load of point mass, we considered the natural length in our calculations since the load did not cause any compression or elongation in the spring due to gravity acting only downwards.