Question
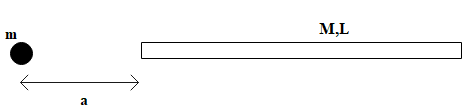
Question: A point mass \(m\) and a uniform thin rod (mass \(M\) and length \(L\)) are shown in figure. Find th...
A point mass m and a uniform thin rod (mass M and length L) are shown in figure. Find the gravitational force of attraction between them.
A.a2GMm
B.a(a+L)GMm
C.(a+L)2GMm
D.(2a+L)24GMm
Solution
Each element of the given rod is not at the same distance from the given point mass. Therefore, the force of gravitation exerted by the rod will not be constant throughout the rod. In such a case, we shall take an infinitesimally small element of the rod and find the force it applies on the point mass. Further, this infinitesimally small force is integrated throughout the length of road to find total force on the point mass.
Complete answer:
Gravitational force on a point mass is given as:
F=r2Gm1m2
Where,
G=6.67×10−11Nm2kg−2 = universal gravitational constant
m1= mass of one body
m2= mass of second body
r= distance between their respective centre of masses
We are given a thin uniform rod of mass M and length L. Let us take an element dx at a distance x from the point mass.

The mass dm of this element is given as:
dm=λ.dx
Where, λ= linear mass density of rod.
∴λ=LM
⇒dm=LM.dx
Therefore, the force on the point by this small element is given as:
dF=x2Gm.dm
We shall now integrate this infinitesimally small force to find the total force on the point mass due to the rod. Since the distance of interaction of rod varies from distance a to (a+L),
