Question
Question: A point mass \[{m_A}\] is connected to a point mass \[{m_B}\] by a massless rod of length \(I\) as s...
A point mass mA is connected to a point mass mB by a massless rod of length I as shown in the figure. It is observed that the ratio of the moment of inertia of the system about the two axes BB and AA, which is parallel to each and perpendicular to the rod, is IAAImm=3. The distance of the centre of mass of the system from the mass A is
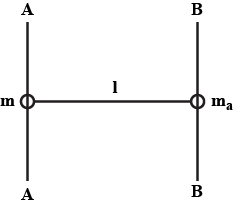
A. (3/4)l
B. (2/3)l
C. (1/2)l
D. (1/4)l
Solution
In this we will put light on a very basic yet very important topic of physics. In this question we will learn about inertia and moment of inertia and the concept behind. We will also study the formulas involved. And hence, this will lead us in approaching our answer.Below here these concepts are explained properly.
Complete step by step answer:
Inertia: As earlier Newton mentioned that every object which is in a particular position will always try to persist that position only. It is there all over universe objects deny any change. This phenomena of denial of any change in their state of motion is named as inertia
It is the opposing quality of any physical object to any difference in its velocity. Not only velocity but changes to the object's speed, or direction of motion. As an outcome of this property is the idea of objects to keep moving in a straight line at a constant speed, when there is an availability of external force.
Inertia can be broken down into the two Latin word, iners, meaning idle, sluggish.
Moment of Inertia: Inertia is a rotational analogue for mass. It is called the moment of inertia of the body about the given axis of rotation. Moment of inertia is the desired rotational motion analogue of mass that is in rotational motion The moment of inertia plays a similar role as mass does in linear motion. It is not a fixed quantity. It depends on orientation and position of the axis of rotation with respect to the body as a whole.
The moment of inertia of rod is determined by formula
IBB=MAl2......................(1) IAA=MBl2.................................(2)
Dividing eq 1 from eq 2
\dfrac{{{I_{AA}}}}{{{I_{BB}}}} = 3 \\\
We get,
3=MB MA=3MB MAXA=MB(l−XA)
We will substitute the value of MA,
3MBXA=MB(l−XA) 3XA=l−XA 4XA=l XA=4l
So, from the equation we can conclude that option (D) is correct.
Hence, the correct answer is option D.
Note:
Moment of inertia depends upon the mass of the body, its shape, its size, distribution of mass about the axis of rotation. It can be also explained as a system’s net angular momentum to its angular velocity around a principal axis. These concepts are useful in solving questions of such kinds.
