Question
Question: A point mass \[{{m}_{0}}\] is placed at a distance \[\dfrac{R}{3}\] from the centre of a spherical s...
A point mass m0 is placed at a distance 3R from the centre of a spherical shell of mass M and radius R. The gravitational force on the point mass m0 is
& \text{A}\text{. }\dfrac{9GM{{m}_{0}}}{{{R}^{2}}} \\\ & \text{B}\text{. }\dfrac{GM{{m}_{0}}}{{{R}^{2}}} \\\ & \text{C}\text{. Zero} \\\ & \text{D}\text{. }\dfrac{4GM{{m}_{0}}}{{{R}^{2}}} \\\ \end{aligned}$$Solution
The gravitational force is the force of attraction due to mass of an object. This force is an attractive force in between two objects with masses placed at some distance from each other. Here the distance is given and by using the gravitational force formula we can find the answer in terms of masses of objects and its distance.
Formula used:
FG=r2GMm
Complete step-by-step answer:
Gravitational force is an attractive force which pulls two objects towards each other due to their masses which attracts each other towards its centre. Suppose two masses M and m are kept at a distance r from each other (as shown in figure), then the gravitational force is given by
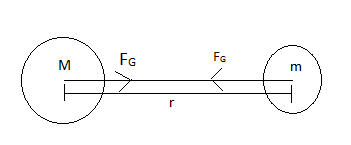
FG=r2GMm
Where G is the gravitational constant.
Now, according to question bodies of masses M and m0 are apart from each other by a distance 3R which can be shown diagrammatically as below.
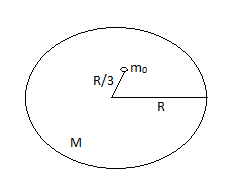
Then the gravitational force will be given as
