Question

A point is selected at random from the interior of the circle. The probability that the point is closer at the centre than the boundary of the circle is:
A. $\dfrac{3}{4}$
B. $\dfrac{1}{2}$
C. $\dfrac{1}{4}$
D. none of these

Answer 1

let us assume the circle of the radius $r$ so now if the point lie within the radius $\dfrac{r}{2}$ then it will be close to the circle then the probability of the point to be closer to the centre will be the ratio of the area of the circle with the radius $\dfrac{r}{2}$ and the area of the circle with the radius $r$.

Complete step by step solution:
Here we are given in the question that we have to select the point from the interior of the circle such that it is closer to the centre. So let us assume the circle of the radius $r$ and the centre O.

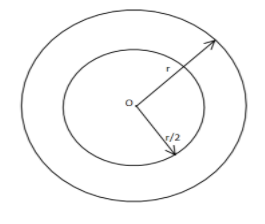
So we need to consider the point such that it is closer to the point O so we draw another concentric circle of the radius $\dfrac{r}{2}$ so that when it lies within the circle of the radius $\dfrac{r}{2}$ then it will be considered
As closest to the centre of the radius$r$.
If it is outside the circle of the radius $\dfrac{r}{2}$ and inside the circle of the radius r then it will be considered closer to the circumference.
We also know that${\text{probability}} = \dfrac{{{\text{number of favourable outcome}}}}{{{\text{total number of outcomes}}}}$
So the number of possible outcomes will be the area of the circle of the radius $\dfrac{r}{2}$ in which the point lies closer to the centre so the possible area$= \pi {\left( {\dfrac{r}{2}} \right)^2}$
Total area would be $\pi {r^2}$
So ${\text{probability}} = \dfrac{{\pi {{\left( {\dfrac{r}{2}} \right)}^2}}}{{\pi {r^2}}} = \dfrac{{{r^2}}}{{4{r^2}}} = \dfrac{1}{4}$

Hence option C is correct.

Note:
We should know that the probability of any two events A and B is given by
$P\left( {\dfrac{A}{B}} \right) = \dfrac{{P(A \cap B)}}{{P(B)}}$ and here $P\left( {\dfrac{A}{B}} \right)$ represents the probability of the occurrence of A if B has already occurred and $P(B)$ is the probability of the occurrence of event $B$