Question
Question: A point is considered at a distance d→ 0 near the bottom most point of a hemispherical surface havin...
A point is considered at a distance d→ 0 near the bottom most point of a hemispherical surface having a uniform charge density σ as shown in figure. The electric field near the curved surface of the hemisphere is nearly.
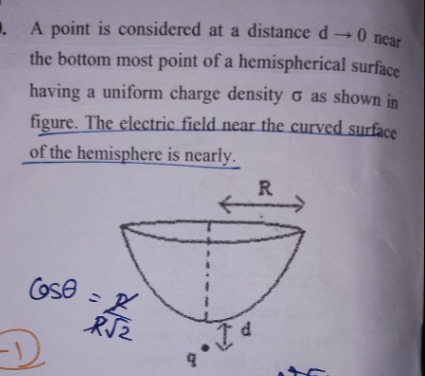
ϵ0σ
2ϵ0σ
4ϵ0σ
0
2ϵ0σ
Solution
When a point is very close to a charged surface with uniform surface charge density σ, the electric field near the surface is approximately equal to the electric field of an infinite plane with the same charge density. This approximation is valid when the distance from the point to the surface is much smaller than the radius of curvature of the surface at that point.
In this problem, the point is considered at a distance d→0 near the bottom-most point of a hemispherical surface. The bottom-most point of a hemisphere is a point on the curved surface. The radius of curvature at this point is R. Since d→0, the distance from the point to the surface is infinitesimally small. Since the distance is much smaller than the radius of curvature R, we can approximate the surface near the bottom-most point as an infinite plane with uniform charge density σ.
The electric field due to an infinite plane with uniform surface charge density σ is given by:
E=2ϵ0σ
The direction of the electric field is perpendicular to the plane, pointing away from the plane if σ>0 and towards the plane if σ<0.
In this case, the point is near the bottom-most point of the curved surface. At the bottom-most point, the tangent plane to the hemisphere is horizontal. The outward normal to the hemisphere at the bottom-most point points downwards (assuming the hemisphere is oriented with the curved surface at the bottom). If the charge density σ is positive, the electric field just outside the surface at the bottom-most point will be directed downwards, perpendicular to the surface, with magnitude 2ϵ0σ. Since the point is at a distance d→0 from the bottom-most point, the electric field at this point is approximately the same as the electric field just outside the surface at the bottom-most point.
Therefore, the magnitude of the electric field near the bottom-most point of the curved surface is approximately 2ϵ0σ.
