Solveeit Logo
Login

Question

Question: A point charge q moves from point P to a point S along a path PQRS in a uniform electric field E poi...

A point charge q moves from point P to a point S along a path PQRS in a uniform electric field E pointing parallel to the x-axis. The coordinates of P, Q, R and S are (a,b,0), (2a,0,0), (a,-b,0) and (0,0,0). The work done by the field in the above process is:
A.Zero
B.qEB
C.qEa
D.-qEa

Explanation

Solution

Recall that the work done is a product of the force and the force-induced displacement in the direction of applied force. Also, electric force is a conservative force, so work done by this force is path independent. Using the above two statements, first determine the component of displacement of the charge that is in the direction of the electric field, and finally determine the work done in the direction of the applied field, i.e., along the x-axis.

Formula Used:
Work done W=F⃗.dr⃗W = \vec{F}.d\vec{r}
Electric force F⃗=qE⃗\vec{F} = q\vec{E}

Complete Solution answer:
We have a point charge q that moves in a path as shown in the figure in a uniform electric field directed along the x-axis E⃗=Ex^\vec{E} = E\hat{x},
Recall that the electric field exerts a coulombic force on the moving point charge. This is given as:
F⃗=qE⃗=qEx^\vec{F} = q\vec{E} = qE\hat{x}
Now, the work done by this force on q is independent of the path taken, and depends only on the initial and final position of the charge in the field. The charge moves from P to Q to R and finally to S. This means that the work done by the force on the charge as it moves from P→Q→R→SP \rightarrow Q \rightarrow R \rightarrow S is same as the work done by the force as if the charge moved from P→SP\rightarrow S.

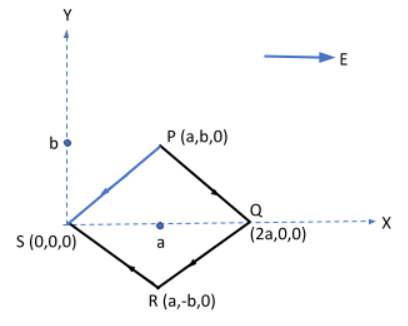
We know that the initial position was P(a,b,0) or (P⃗=ax^+by^+0z^\vec{P} = a\hat{x}+b\hat{y}+0\hat{z}), and the final position was S(0,0,0) or (S⃗=0x^+0y^+0z^\vec{S}=0\hat{x}+0\hat{y}+0\hat{z}). In such a case, the displacement vector of the charge q will be difference in the position vectors at P and S:
r⃗=PS⃗=S⃗−P⃗=(0x^+0y^+0z^)–(ax^+by^+0z^)\vec{r} = \vec{PS} = \vec{S} - \vec{P} = (0\hat{x}+0\hat{y}+0\hat{z}) – (a\hat{x}+b\hat{y}+0\hat{z})
⇒r⃗=−ax^−by^\Rightarrow \vec{r} = -a\hat{x}-b\hat{y}
Therefore, the work done by the force can be given as:
Work done W=F⃗.r⃗=q(Ex^).(−ax^−by^)=q(E)(−a)=−qEaW = \vec{F}.\vec{r} = q(E\hat{x}).(-a\hat{x}-b\hat{y}) = q (E)(-a) = -qEa

Therefore, the correct choice would be D. -qEa

Note:
It is important to remember the distinction between conservative and non-conservative forces. A conservative force “conserves” the energy of the system by not spending it on collateral processes, whereas a non-conservative force does not shy away from energy expenditures on such processes via heat, sound, light, etc.
Irrespective of the fact that work done is generally a path function, the work done by a conservative force is independent of the path taken and depends only on the initial and final position of the body whereas the work done by a non-conservative force is dependent on the path taken. Note that if the path taken by an object is closed, then the work done by a conservative force is zero, since the displacement of the object is zero.