Question

A point charge Q lies on the perpendicular bisector of an electric dipole of dipole p. If the distance of Q from the dipole is r (much larger than the size of the dipole), then the electric field at $\theta$ is proportional to:
A. ${P^2}$ and ${r^{ - 3}}$
B. ${P^2}$ and ${r^{ - 2}}$
C. ${P^{ - 1}}$ and ${r^{ - 3}}$
D. $P$ and ${r^{ - 3}}$

Answer 1

Express the electric field at point charge Q. It will have only a horizontal component of electric field. In the expression, neglect the higher term of dipole distance. Use the expression for dipole moment , $p = qa$, where, q is the charge and a is the dipole distance.

Formula used:
The electric field at a distance r from the point charge q is expressed as,
$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{r^2}}}$
Here, ${\varepsilon _0}$ is the permittivity of the free space.

Complete step by step answer:
We have given that the point charge Q lies on the perpendicular bisector and the distance between the point charge Q and dipole is much larger than the size of the dipole as shown in the figure below.

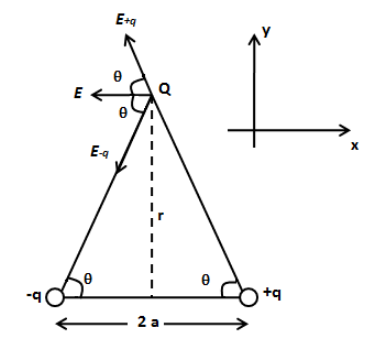
In the above figure, ${E_{ - q}}$ is the electric field due to charge $- q$ and ${E_{ + q}}$ is the electric field due to charge $+ q$. The vertical component of ${E_{ - q}}$ is along the negative y-axis and vertical component of ${E_{ + q}}$ is along the positive y-axis. Hence we can say they cancel out. Now, the net electric field of the dipole at point charge Q is due the horizontal components of ${E_{ + q}}$ and ${E_{ - q}}$. Therefore, we see that the electric field at $\theta$ is the sum of horizontal components of ${E_{ + q}}$ and ${E_{ - q}}$.

We can express the magnitude of electric field at point charge Q due to charge $- q$ as follows,
$\left| {{E_{ - q}}} \right| = k\dfrac{q}{{{r^2} + {a^2}}}$ …… (1)
Here, k is the constant and it has the value $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$.
We can express the magnitude of electric field at point charge Q due to charge $+ q$ as follows,
$\left| {{E_{ + q}}} \right| = k\dfrac{q}{{{r^2} + {a^2}}}$ …… (2)

Since the electric field at Q is the sum of horizontal components of electric field along the negative x-axis, we can write,
$\vec E = \left| {{E_{ + q}}} \right|\cos \theta \left( { - \hat i} \right) + \left| {{E_{ - q}}} \right|\cos \theta \left( { - \hat i} \right)$
$\Rightarrow \vec E = k\dfrac{q}{{{r^2} + {a^2}}}\cos \theta \left( { - \hat i} \right) + k\dfrac{q}{{{r^2} + {a^2}}}\cos \theta \left( { - \hat i} \right)$
$\Rightarrow \vec E = k\dfrac{{2q}}{{{r^2} + {a^2}}}\cos \theta \left( { - \hat i} \right)$ …… (3)
From the trigonometry of the above figure, we can express the $\cos \theta$ as follows,
$\cos \theta = \dfrac{a}{{\sqrt {{r^2} + {a^2}} }}$
Therefore, we can rewrite equation (3) as,
$\vec E = k\left( {\dfrac{{2q}}{{{r^2} + {a^2}}}} \right)\left( {\dfrac{a}{{\sqrt {{r^2} + {a^2}} }}} \right)\left( { - \hat i} \right)$
$\Rightarrow \vec E = k\dfrac{{2qa}}{{{{\left( {{r^2} + {a^2}} \right)}^{3/2}}}}\left( { - \hat i} \right)$
But we know that the dipole moment of an electric dipole is expressed as,
$\hat P = qa\,\hat i$
Therefore, the above equation becomes,
$\vec E = - k\dfrac{{2P}}{{{{\left( {{r^2} + {a^2}} \right)}^{3/2}}}}$
Now, we have given that the distance h is very much larger than the distance a. Therefore, we can neglect the term ${a^2}$ in the denominator.
$\vec E = - k\dfrac{{2P}}{{{{\left( {{r^2}} \right)}^{3/2}}}}$
$\therefore \vec E = - k\dfrac{{2P}}{{{r^3}}}$
Thus, from the above equation, we can infer that the electric field is proportional to P and ${r^{ - 3}}$.

So, the correct answer is option D.

Note: Remember, dipole moment is a vector quantity which directs from negative charge to positive charge along the dipole. In our solution, since the dipole is along the positive x-axis, we have expressed it as $\hat P = qa\,\hat i$. If the negative charge is on the right side and positive on the left, we would have $\hat P = qa\left( { - \,\hat i} \right)$.