Question

A point charge q is situated at a distance r from one end of a thin conducting rod of length L having a charge Q (uniformly distributed along its length). Find the magnitudes of electric force between the two.
A) $\dfrac{{KQq}}{{{r^2}}}$
B) $\dfrac{{2KQ}}{{r(r + L)}}$
C) $\dfrac{{KQq}}{{r(r - L)}}$
D) $\dfrac{{KQq}}{{r(r + L)}}$

Answer 1

We can draw the diagram according to the question, then consider a small part on the rod where the force exerted by the two charges will be calculated and after applying the concept of electric force, we will obtain the desired result.

Formula used:
Formula for electric force between the two charges is:
$F = K\dfrac{{{q_1}{q_2}}}{{{r^2}}}$ where,
F = Force acting on the body
${q_1}$ = magnitude charge 1
${q_2}$ = magnitude charge 1
K = proportionality constant.

Complete step by step answer:

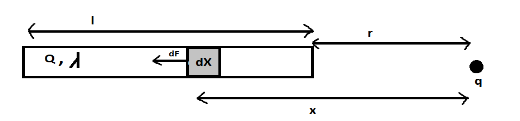
The conducting rod has length L and charge Q, at a distance r from this rod, a charge q is present.
Let the linear charge density of this rod be $\lambda$, so:
$\lambda = \dfrac{Q}{L}$ _________ (1)
Because linear charge density is defined as the quantity of charge per unit length
From q, at distance x, a part dx of the rod having charge dQ (small part of Q) is considered.
Q = dQ
L = dx
Substituting these values in (1)

$$\lambda = \dfrac{Q}{L} \\\ \Rightarrow Q = \lambda L \\\ \Rightarrow dQ = \lambda dx \\\$$

Now,
$dQ = \dfrac{Q}{L}dx$ [since of 1] ________ (2)
Force between two charges is given as:
The force between the two charges is directly proportional to the product of magnitude of their charges and inversely proportional to the square of the distance between them.
$F \propto \dfrac{{{q_1}{q_2}}}{{{r^2}}}$ or
$F = K\dfrac{{{q_1}{q_2}}}{{{r^2}}}$
Here,
F = dF (acting on the small considered part)
${q_1}$ = dQ
$\Rightarrow{q_2}$ = q
r = x (distance from q)
Substituting these values, we get:
$dF = K\dfrac{{dQ.q}}{{{x^2}}}$
Substituting the value of dQ from (2):
$dF = K\dfrac{q}{{{x^2}}}.\dfrac{Q}{L}dx$
We have to calculate this force ranging from r to r + L, for that, we need to integrate both the sides:
$\int {dF = \int\limits_r^{r + L} {K\dfrac{q}{{{x^2}}}.\dfrac{Q}{L}dx} }$
Taking the constants out, we get:
$F = \dfrac{{KQq}}{L}\int\limits_r^{r + L} {\dfrac{1}{{{x^2}}}} \\\$
$\int {\dfrac{1}{{{x^2}}}} \to \int {{{(x)}^{ - 2}}} \\\ \Rightarrow\int {\dfrac{1}{{{x^2}}}}= \dfrac{{{{(x)}^{ - 2 + 1}}}}{{ - 2 + 1}} \\\ \Rightarrow\int {\dfrac{1}{{{x^2}}}}= {( - x)^{ - 1}} \\\ \Rightarrow\int {\dfrac{1}{{{x^2}}}}= \left[ { - \dfrac{1}{x}} \right] \\\$
Substituting:
$F = \dfrac{{KQq}}{L}\left[ { - \dfrac{1}{x}} \right]_r^{r + L} \\\ \Rightarrow F = \dfrac{{KQq}}{L}\left[ {\dfrac{1}{r} - \dfrac{1}{{r + L}}} \right] \\\ \Rightarrow F = \dfrac{{KQq}}{L} \times \dfrac{{r + L - r}}{{r(r + L)}} \\\ \therefore F = \dfrac{{KQq}}{{r(r + L)}} \$
Therefore, the magnitudes of electric force between the two charges is $\dfrac{{KQq}}{{r(r + L)}}$ and the correct option is D).

Note: For integration, remember:
$\int {{x^n}dx = \dfrac{{{x^{n + 1}}}}{{n + 1}}}$
After integration with limits, the higher substituted limit (written at top on sign) is subtracted from the lower substituted limit (written at bottom on sign)
The value of K in $F = K\dfrac{{{q_1}{q_2}}}{{{r^2}}}$ is $\dfrac{1}{{4\pi {\varepsilon _0}}}$