Question

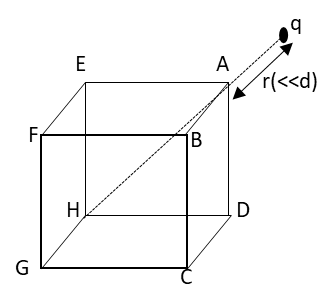
A point charge $+ q$ is placed on the line through AH and just outside the cube (of side $d$) at a distance of ‘$r$’ ($r < < d$) from ‘A’. Total flux of electric field through the surface ABCD is

A.$\dfrac{{ - q}}{{8{\varepsilon _0}}}$
B.$\dfrac{q}{{16{\varepsilon _0}}}$
C.$\dfrac{q}{{8{\varepsilon _0}}}$
D.$\dfrac{{ - q}}{{16{\varepsilon _0}}}$

Answer 1

Use the formula for flux of electric field passing through a surface. Construct a Gaussian surface for the surface ABCD of the cube. Determine the total flux through this Gaussian surface and from these calculations determine the flux passing though the surface ABCD and its direction.

Formula used:
The magnetic flux $\phi$ through a Gaussian sphere is given by
$\phi = \dfrac{q}{{{\varepsilon _0}}}$ …… (1)
Here, $q$ is the charge and ${\varepsilon _0}$ is permittivity of free space.

Complete step by step answer:
We have given that a point charge $+ q$ is placed at a distance $r$ from the cube along the line through AH.
The length of each side of the cube is $d$.
We have asked to determine the total flux of electric field through the surface ABCD of the cube.
But we know that the electric flux is always through a Gaussian surface i.e. a closed surface and ABCD is not a close surface.
Hence, let us draw a Gaussian surface including the surface ABCD of the given cube as follows:

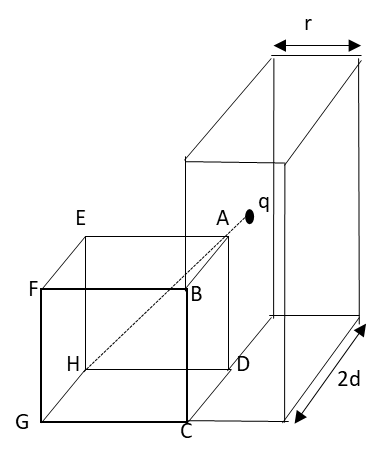
Now the above constructed surface around the surface ABCD is a Gaussian surface of sides of cube as $2d$ and $r$. Since the charge q is positive, the magnetic flux due to electric field is outward from the charge q from all the surfaces of the new Gaussian surface.
Since the length $r$ is very small, the flux passing through the sides of length $r$ can be neglected.
Hence, there remains only two surfaces of the Gaussian surface with sides $2d$ each.
Hence, the total flux $\phi$ passing through the whole Gaussian surface is twice the flux ${\phi _{2d}}$ passing through two squares of with side $2d$.
$\phi = 2{\phi _{2d}}$
Also, the flux ${\phi _{ABCD}}$ passing through the surface ABCD is one fourth of the flux ${\phi _{2d}}$ passing though one square of side $2d$.
${\phi _{ABCD}} = \dfrac{1}{4}{\phi _{2d}}$
Substitute $\dfrac{\phi }{2}$ for ${\phi _{2d}}$ in the above equation.
${\phi _{ABCD}} = \dfrac{1}{4}\dfrac{\phi }{2}$
$\Rightarrow {\phi _{ABCD}} = \dfrac{\phi }{8}$
Substitute $\dfrac{q}{{{\varepsilon _0}}}$ for $\phi$ in the above equation.
$\Rightarrow {\phi _{ABCD}} = \dfrac{q}{{8{\varepsilon _0}}}$
$\Rightarrow {\phi _{ABCD}} = \dfrac{{ - q}}{{8{\varepsilon _0}}}$
The negative sign indicates that the direction of the total flux is in the negative direction.
Therefore, the magnetic flux passing through the surface ABCD is $\dfrac{{ - q}}{{8{\varepsilon _0}}}$.

So, the correct answer is “Option A”.

Note:
The students may think how the direction of the flux through the surface ABCD is in a negative direction. But we know that the direction of the flux due to positive charge is outward on all surfaces. Hence, the direction of flux for surface ABCD will be outwards from charge in the left hand direction which is the negative direction.