Question

A point charge $+Q$ is placed just outside an imaginary hemispherical surface of radius $R$ as shown in figure. Which of the following statements is/are correct?

(A) The electric flux passing through the curved surface of the hemisphere is $-\dfrac{Q}{2{{\varepsilon }_{0}}}\left( 1-\dfrac{1}{\sqrt{2}} \right)$
(B) The component of the electric field normal to the flat surface is constant over the surface
(C) Total flux through the curved and the flat surfaces is $\dfrac{Q}{{{\varepsilon }_{0}}}$
(D) The circumference of the flat surface is an equipotential

Answer 1

To find electric flux we use Gauss’ Law. Electric flux is the measure of the electric field through a given area. The electric flux ${{\phi }_{E}}$ through any closed surface is equal to $\dfrac{1}{{{\varepsilon }_{0}}}$ times the net charge $Q$ closed by the surface.

Complete step by step solution:
Given: radius of the hemisphere is $R$
The solid angle subtended by the flat surface at $\Omega =2\pi (1-\cos \theta )$ $...(\text{i})$

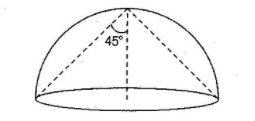
From the above figure, we can say that $\theta ={{45}^{\circ }}$
Flux passing through curved surface is given by,
$\phi =-\dfrac{Q}{{{\varepsilon }_{0}}}\times \dfrac{\Omega }{4\pi }$ $...(\text{ii})$
Put the value of equation $(\text{i})$ in equation $(\text{ii})$, we get
$\phi =-\dfrac{Q}{{{\varepsilon }_{0}}}\times \dfrac{2\pi \left( 1-\dfrac{1}{\sqrt{2}} \right)}{4\pi }$
$\phi =-\dfrac{Q}{2{{\varepsilon }_{0}}}\left( 1-\dfrac{1}{\sqrt{2}} \right)$
Hence, the option (A) is correct.
The component of electric field normal to the flat surface is $E\cos \theta$.

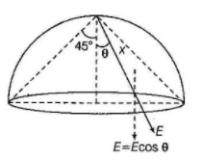
Here $E$ and $\theta$ changes for different points on the flat surface. Therefore option (B) is incorrect.
The total flux due to charge $Q$ is $\phi$ and $\phi$ through the curved and flat surface will be less than $\dfrac{Q}{{{\varepsilon }_{0}}}$. Hence option (C) is incorrect.
Potential at any point on the circumference of the flat surface is given by,
$V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{\sqrt{{{R}^{2}}+{{R}^{2}}}}$
$V=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{Q}{\sqrt{2}R}$
Since, the circumference is equidistant from charge $Q$ it will be an equipotential surface.

Therefore option (D) is correct.

Note: An equipotential surface is that at every point electrical potential is the same. The electric field $\vec{E}$ is directed perpendicular to the equipotential surface. Work done in moving charge over an equipotential surface is zero. Two equipotential surfaces can never intersect.