Question

A point charge Q is placed at distance 2R from the centre, on the axis of charged ring (charge Q) of radius R as shown. The electric potential at point Pis

Answer 1

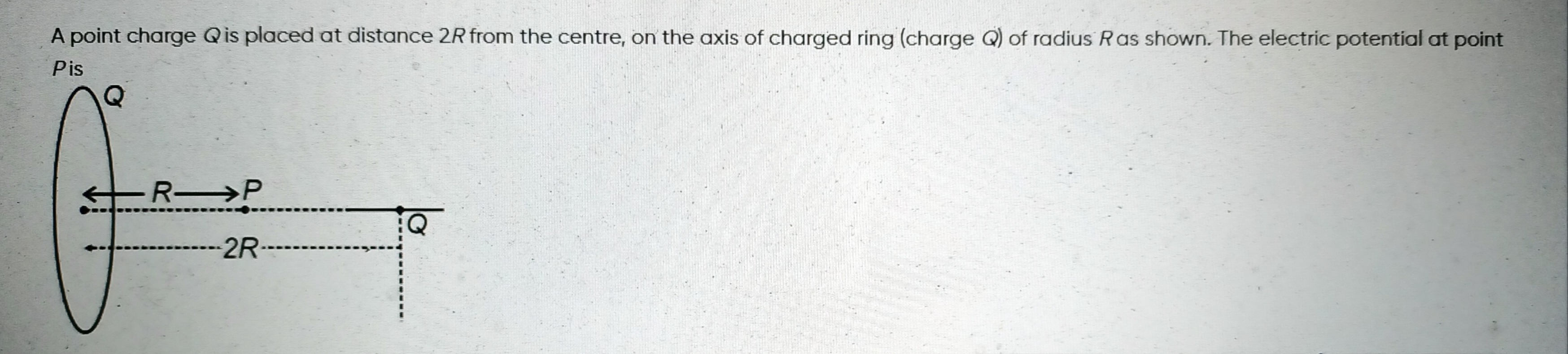
The electric potential at point P is $\frac{Q}{4\pi\epsilon_0 R} \left( 1 + \frac{1}{\sqrt{2}} \right)$

Answer 2

The problem asks for the electric potential at point P due to a charged ring and a point charge. Electric potential is a scalar quantity, so we can find the potential due to each charge distribution separately and then sum them up.

1. Electric Potential due to the Charged Ring at Point P: The ring has a total charge Q and radius R. Point P is located on the axis of the ring at a distance R from its center. The formula for the electric potential on the axis of a uniformly charged ring at a distance $x$ from its center is given by: $V_{ring} = \frac{kQ}{\sqrt{R_{ring}^2 + x^2}}$ Here, $R_{ring} = R$ (radius of the ring) and $x = R$ (distance of P from the center of the ring). Substituting these values: $V_{ring} = \frac{kQ}{\sqrt{R^2 + R^2}} = \frac{kQ}{\sqrt{2R^2}} = \frac{kQ}{R\sqrt{2}}$ Where $k = \frac{1}{4\pi\epsilon_0}$ is Coulomb's constant. So, $V_{ring} = \frac{Q}{4\pi\epsilon_0 R\sqrt{2}}$

2. Electric Potential due to the Point Charge at Point P: A point charge Q is placed on the axis at a distance 2R from the center of the ring. Point P is also on the axis at a distance R from the center of the ring. Since both are on the same side of the ring's center (as indicated by the diagram), the distance between the point charge Q and point P is: $d = 2R - R = R$ The formula for the electric potential due to a point charge is: $V_{point\_charge} = \frac{kQ}{d}$ Substituting the distance $d = R$: $V_{point\_charge} = \frac{kQ}{R}$ Or, $V_{point\_charge} = \frac{Q}{4\pi\epsilon_0 R}$

3. Total Electric Potential at Point P: The total electric potential at point P is the sum of the potentials due to the ring and the point charge: $V_P = V_{ring} + V_{point\_charge}$ $V_P = \frac{Q}{4\pi\epsilon_0 R\sqrt{2}} + \frac{Q}{4\pi\epsilon_0 R}$ Factor out the common term $\frac{Q}{4\pi\epsilon_0 R}$: $V_P = \frac{Q}{4\pi\epsilon_0 R} \left( \frac{1}{\sqrt{2}} + 1 \right)$ To simplify the expression, we can rationalize $\frac{1}{\sqrt{2}}$ by multiplying the numerator and denominator by $\sqrt{2}$: $\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$. $V_P = \frac{Q}{4\pi\epsilon_0 R} \left( 1 + \frac{\sqrt{2}}{2} \right)$