Question
Question: A point charge \(q\) is located at the center of a thin ring of radius \(R\) with uniformly distribu...
A point charge q is located at the center of a thin ring of radius R with uniformly distributed charge −q. Find the magnitude of the electric field strength vector at the point lying on the axis of the ring at a distance x from its center if x>>R.
Solution
The net electric field strength at the point lying on the axis of the ring at a distance x is equal to the sum of electric field strengths at that point due to the point charge q at the center of the ring, as well as the ring of uniformly distributed charge −q, itself. Since x>>R, binomial approximation can be used while simplifying this net electric field strength.
Formula used:
1)Ec=x2kq
2)Er=(x2+R2)23−kqx
3)EP=Ec+Er
Complete answer:
We are provided with a point charge q, located at the center of a thin ring of radius R with uniformly distributed charge −q. We are required to find the magnitude of the electric field strength vector at a point lying on the axis of the ring at a distance x from its center, if x>>R.
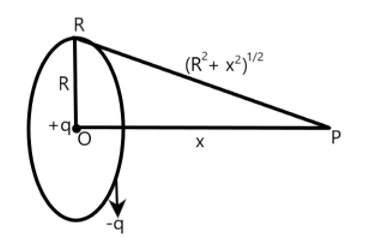
From the diagram given above, it is clear that we have to find the magnitude of electric field strength at point P. Also, the center of the ring where a charge q is located is denoted as O. The distance between center of the ring O and the point on the axis of the ring P is given by
OP=x
and radius of the ring OR is given by
OR=R
Now, if we draw a right triangle ORP, then
RP=(R2+x2)21
where
RP is the distance of the ring from the point lying on the axis of the ring
The net electric field strength at the point (P), lying on the axis of the ring at a distance x is equal to the sum of electric field strengths at that point due to the point charge q at the center of the ring as well as the ring of uniformly distributed charge −q, itself.
If Ec denotes the electric field string at P due to charge qat the center of the ring, then, Ec is given by
Ec=x2kq
where
Ec is the electric field string at point P due to charge q
k=4πε01, is the electrostatic constant
q is the point charge on the center of the ring O
x is the distance between the center of the ring and the point P, lying on the axis of the ring (=OP)
Let this be equation 1.
Similarly, if Er represents the electric field strength at P due to the ring of uniformly distributed charge q, then, Er is given by
Er=(x2+R2)23k(−q)x=(x2+R2)23−kqx
where
Er is the electric field string at point P due to the ring of uniformly distributed charge −q
k=4πε01, is the electrostatic constant
x is the distance between the center of the ring and the point P, lying on the axis of the ring (=OP)
R is the radius of the ring (=OR)
Let this be equation 2.
Now, using equation 1 and equation 2, we have
EP=Ec+Er=x2kq−(x2+R2)23kqx
where
EP is the net electric field strength at point P
Let this be equation 3.
Simplifying equation 3, we have
EP=x2kq−(x2+R2)23kqx=x3kqx−(1+(xR)2)23x=x2kq1−(1+(xR)2)−23
Now, we are given that x>>R. Therefore, we have
x>>R⇒xR<<1
Hence, we can use the binomial approximation given by
(1+a)−n=1−na for a>1
in the above equation.
Using this binomial approximation in the above simplification of EP, we have
EP=x2kq1−(1+(xR)2)−23=x2kq(1−(1−23(xR)2))=x2kq(1−1+23(xR)2)=2x43kqR2
Let this be equation 4.
Substituting the expression for electrostatic constant k=4πε01 in equation 4, we have
EP=2x43kqR2=8πε0x43qR2
Therefore, if x>>R, the magnitude of electric field strength vector at a point lying on the axis of the ring ( of uniformly distributed charge −q), at a distance x from its center (of charge q) is equal to 8πε0x43qR2.
Note:
Students need to be aware of the formula for electric field strength due to a ring or a coil, at a point on the axis of the ring or the coil. As already mentioned, it is given by
E=(x2+R2)23kqx
where
E is the electric field strength due to a ring carrying a charge q at a point on the axis of the ring
x is the distance of the point on the axis of the ring from the center of the ring
R is the radius of the ring
k=4πε01, is the electrostatic constant
This is a standard definition and can be easily derived by considering a small charge element (dq)on the ring and deducing the electric field strength due to this charge element at a point on the axis of the ring. Integrating this field strength over the circumference of the ring will give the expression for field strength due to the whole ring at this point on its axis, as given above.
