Question
Question: A point charge \(q = 24{\varepsilon _0}\) Coulomb is kept above the midpoint of the edge of length \...
A point charge q=24ε0 Coulomb is kept above the midpoint of the edge of length 2a as shown in the figure. Line AB is perpendicular to the plane of the rectangle. Find the flux through the rectangle shown in the figure.
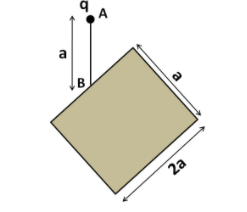
Solution
To solve this question, we need to use the gauss theorem. For this, we need to place the given charge in a closed volume, which has to be generated by using the rectangles given in the question. Then by using the unitary method we can find out the value of required flux through the given rectangle.
Complete step-by-step solution:
We know from the Gauss theorem that the total flux through a closed surface due to a point charge placed within it is given by
φ=ε0q................(1)
So we have to enclose the given point charge within a closed surface, symmetrically. We start by placing a similar rectangle adjacent to the given rectangle, so that the point charge is directly above the centre of the square thus formed, as shown in the figure below.
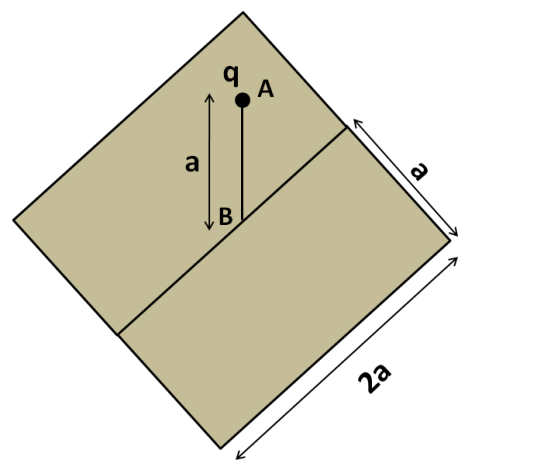
So now we have our point charge placed at above the centre of the square of side 2a.
For generating a closed volume, we have to place five additional such squares of side 2a to form a cube of side 2a. The charge will be symmetrically inside the cube. So from (1) the flux passing from this cube is
φ=ε0q
As the charge is symmetrically present within the cube, so the flux through each of the squares of side 2a is the same. As we have a total of six such squares, so the flux passing through the base square is
φ′=6ε0q
Now, the base square of side 2a is made by placing two rectangles of dimensions 2a×a. As the charge is symmetrically placed with respect to their combination, as shown in the above figure, the flux passing through each of these rectangles is
φ′′=12ε0q
According to the question, q=24ε0C. Substituting this above, we finally get
φ′′=2Nm2/C
Hence, the flux through the given rectangle is equal to 2Nm2/C.
Note: The application of the gauss theorem does not depend on the symmetric placement of the charge within the closed surface. The charge just needs to be present within it. But for calculating the flux through a particular portion of the closed surface, we need the symmetry.
