Question
Question: A point charge \({{q}_{1}}=+2\mu C\) is placed at the origin of coordinates. A second charge, \({{q}...
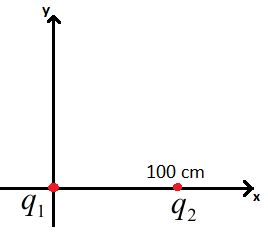
A point charge q1=+2μC is placed at the origin of coordinates. A second charge, q2=−3μC, is placed on the x-axis at x = 100cm. At what point (or points) on the x-axis will the absolute potential be zero?
A. x = 40cm and x = –200cm
B. x = 40cm only
C. x = –200cm only
D. x = 80cm only
Solution
We are given two charges and their position coordinates. To find the point where the electric potential is zero we need to find the electric potential at that point due to both charges separately. Since the total potential is zero we can equate both potentials and thus we get the solution.
Formula used:
Electric potential, V=rkq .
Complete step-by-step answer:
In the question we are given two point charges and the positions of these charges are also given.
Charge q1=+2μC and charge q2=−3μC
The position of charge ‘q1 is at origin and the position of charge ‘q2’ is on the x axis at 100 cm = distance.
We need to find the points on the x – axis where the absolute potential has the value zero.
To find this we know the equation for potential is,
V=rkq, where ‘V’ is the electric potential, ‘k’ is a constant, ‘q’ is the charge and ‘r’ is the distance of separation.
Now let us consider a point where the net electric potential is zero and let the distance from ‘q1’ to this point be ‘r1’ and distance from ‘q2’ to this point be ‘r2’.
Then the electric potential at this region due to the charge ‘q1’can be written as,
V1=r1kq1
And the electric potential at this point due to the charge ‘q2’ can be written as,
V2=r2kq2
We assumed that the electric potential at this point is zero. We know that for the electric potential experienced due to two charges to be zero, V1 and V2 must be equal to each other.
Therefore,
⇒V1+V2=0
⇔V1=−V2
⇒r1kq1=−r2kq2
Since we know the values of ‘q1’ and ‘q2’ we can substitute them in the above equation.
⇒r12k=−r2−3k
⇒r12k=r23k
Since ‘k’ is a constant and is the same value we can eliminate ‘k’.
⇒r12=r23
Thus we get the ratio of the distance of separation as,
⇒r2r1=32
Consider the figure below.
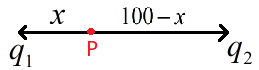
In this ‘P’ is the point at which the potential is zero.
In the question we are given that the distance from ‘q1’ to ‘q2’ is 100cm.
Now let us take the distance from ‘q1’ to ‘P‘ as ‘x’ then the distance from ‘P’ to ‘q2’ will be (100 – x), i.e. here r1=x and r2=100−x
From the earlier calculations we know that,
r2r1=32⇒2r2=3r1
Therefore we can write,
2(100−x)=3x⇒2(100−x)−3x=0
⇒200−2x−3x=0
⇒200=5x
⇒x=5200
⇒x=40cm
Hence the distance from origin to the point ‘P’ is 40 cm.
Now let us consider the figure below,
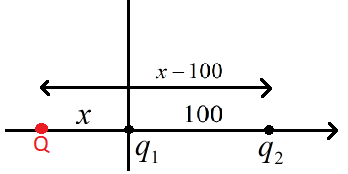
There is another point ‘Q’ on the x – axis in the negative ‘x’ direction.
Let the distance from ‘q1’ to ‘Q’ be ‘x’ then the distance from ‘q2’ to ‘Q’ will be (x-100), i.e.
r1=x
r2=(x−100)
Since 2r2=3r1, we can write
⇒2(x−100)=3x
⇒2x−200=3x
⇒2x−3x=200
⇒−x=200
⇒x=−200cm
Thus we have the distance from origin to the point ‘Q’ as – 200cm.
Therefore at points x = 40cm and x = – 200cm the potential will be zero.
So, the correct answer is “Option A”.
Note: Electric potential or voltage is simply the difference in potential energy per unit charge between two points in an electric field. It can also be stated as the work done in moving a unit electric charge from one point to another.
When we solve for the distance to point ‘P’, we get x = 40 cm. there we do not consider (100-x) because it is not the distance from the origin to the point ‘P’. We are asked to find the position of the point with zero electric potential. We know that when we consider position we take distance from origin.
Similarly while solving for ‘Q’, we do not consider (100 – x).
