Solveeit Logo
Login

Question

Question: A point charge of \(6 \times {10^{ - 8}}C\) is situated at the coordinate origin. How much work will...

A point charge of 6×10−8C6 \times {10^{ - 8}}C is situated at the coordinate origin. How much work will be done in taking an electron from the point x = 3m to x = 6m?
A) 1.44×10−17J1.44 \times {10^{ - 17}}J
B) 1.44×10−27J1.44 \times {10^{ - 27}}J
C) 1.44×10−37J1.44 \times {10^{ - 37}}J
D) 1.44×10−7J1.44 \times {10^{ - 7}}J

Explanation

Solution

The work done in moving electrons can be given by the difference between electric potentials at the two given points caused by the charge placed at the origin. The charge on an electron is −1.6×10−19C - 1.6 \times {10^{ - 19}}C, a negative sign because electrons are negatively charged.

Complete Step by step answer: The given charge 6×10−8C6 \times {10^{ - 8}}C is initially situated at x = 3m, say position A, and we need to calculate the work done in moving it to the point x = 6m, say position B.

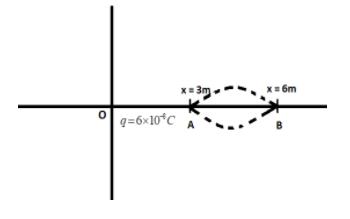
The work done in moving an electron from one point to another is equal to the difference between the electric potential at the two points:
⇒VB−VA=We\Rightarrow {V_B} - {V_A} = \dfrac{W}{e} ________ (1)
Electric potential due to the charge at the origin is given as:
V=q4πε0xV = \dfrac{q}{{4\pi {\varepsilon _0}x}}, where q is the charge and x is the position (or distance). The value of 14πε0\dfrac{1}{{4\pi {\varepsilon _0}}} is 9×109Nm2/C29 \times {10^9}N{m^2}/{C^2}.
At point A:
Charge (q) = 6×10−8C6 \times {10^{ - 8}}C (given)
Distance from the origin (x) = 3
⇒VA=9×109×6×10−8C3 ⇒VA=180  \Rightarrow {V_A} = \dfrac{{9 \times {{10}^9} \times 6 \times {{10}^{ - 8}}C}}{3} \\\ \Rightarrow {V_A} = 180 \\\
At point B:
Charge (q) = 6×10−8C6 \times {10^{ - 8}}C (given)
Distance from the origin (x) = 6
⇒VA=9×109×6×10−8C6 ⇒VA=90  \Rightarrow {V_A} = \dfrac{{9 \times {{10}^9} \times 6 \times {{10}^{ - 8}}C}}{6} \\\ \Rightarrow {V_A} = 90 \\\
The value of charge e on an electron is −1.6×10−19C - 1.6 \times {10^{ - 19}}C. We can find the work done by using equation (1)
VB−VA=We{V_B} - {V_A} = \dfrac{W}{e}
Substituting the known values, we get:
180−90=W−1.6×10−19C ⇒W=−90×1.6×10−19C ⇒W=−1.44×10−17J  180 - 90 = \dfrac{W}{{ - 1.6 \times {{10}^{ - 19}}C}} \\\ \Rightarrow W = - 90 \times 1.6 \times {10^{ - 19}}C \\\ \Rightarrow W = - 1.44 \times {10^{ - 17}}J \\\
The magnitude of this work is 1.44×10−17J1.44 \times {10^{ - 17}}J.

Therefore, the work will done in taking an electron from the point x = 3m to x = 6m is 1.44×10−17J1.44 \times {10^{ - 17}}J

Note: Note that the work done does not depend on the path that is taken to move the electron from one place to another. When the same number with different powers are multiplied, the powers are added and when divided, the powers are subtracted.
Magnitude means the basic value, it does not depend on the sign, even for the negative quantity, the magnitude is positive.