Question
Question: A point charge is placed at the corner of a cube. The electric flux through the shaded surface is ...
A point charge is placed at the corner of a cube. The electric flux through the shaded surface is
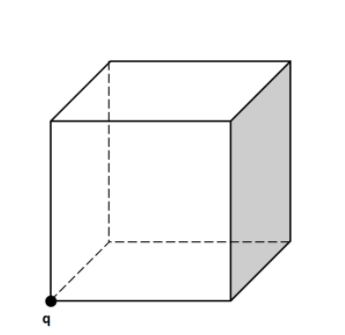
(A) 8ε0q
(B) ε0q
(C) 24ε0q
(D) 12ε0q
Solution
To solve this question, we need to use the Gauss theorem. For that we need to place the charge symmetrically within a closed surface, which must be generated by using the similar cubes as given in the question. Then, using the unitary method, we can determine the required flux.
Complete step by step solution:
We know from the gauss theorem that the total flux passing through a closed surface, within which a charge is enclosed, is given by
φ=ε0q
In the figure given in the question, the charge is placed at the corner of the cube, not within the cube. So we need to enclose it within a closed surface, so that the Gauss theorem can be applied.
So we place three more cubes, similar to the one given in the question around the given charge, as shown in the figure below.
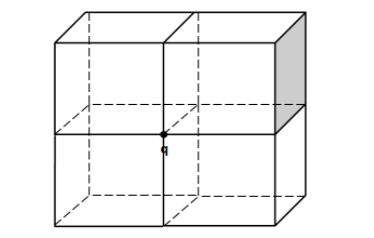
As we can clearly see in the above figure, that now also the charge is not enclosed. This is because the charge is kept at the outer surface of the cuboid, not within it. So we have to take a similar bigger cuboid and keep it on the outer surface of the cuboid, so that the charge is enclosed within the bigger cube thus formed.
As the charge is enclosed in the bigger cube, so the total flux passing through it is given by
φ=ε0q …………………….(1)
Since the bigger cube is composed of two cuboids, and the charge is symmetrically placed with respect to both of them, so the flux passing through each of the cuboids is
φ′=2φ
From (1)
φ′=2ε0q ………………….(2)
So the flux passing through the cuboid shown in the above figure is equal to 2ε0q.
Now, the cuboid is composed of eight cubes, and the charge is placed symmetrically with respect to all of them, so the flux passing through each of these four cubes is given by
φ′′=4φ′
From (2)
φ′′=41×2ε0q
⇒φ′′=8ε0q ………………...(3)
So the flux passing through the given cube is equal to 8ε0q.
We know that a cube has a total of six faces. But the flux will not pass through each of these faces.
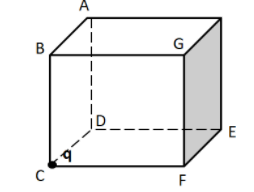
As can be seen in the above figure, the point charge placed at the corner C is touching the three faces of the cube, namely ABCD, CDEF, and BGFC. So the electric field through the charge will not be able to cut through these three faces. Therefore, the flux through all of these three faces will be equal to zero. Hence, the flux will pass through the rest of the three faces of the cube. Therefore, the flux passing through each of these three faces is given by
φ′′′=3φ′′
From (3)
φ′′′=31×8ε0q
⇒φ′′′=24ε0q
The shaded region given in the question is nothing but a face of the cube. So the flux passing through the shaded region is equal to 24ε0q.
Hence, the correct answer is option (C).
Note: We should not forget the fact that the flux passing through the surfaces, which the charge is touching, will be equal to zero. The electric field through the point charge will be parallel to these faces.
