Question
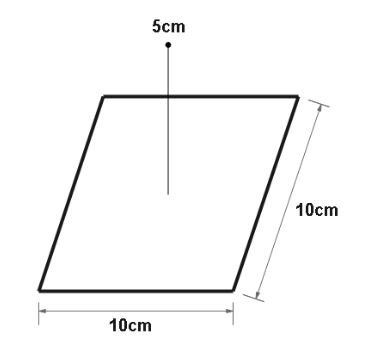
Question: A point charge \[ + 10\mu C\] is a distance \(5\,cm\) directly above the centre of a square of side ...
A point charge +10μC is a distance 5cm directly above the centre of a square of side 10cm , as shown. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with an edge 10cm .)
Solution
To solve this question, one must know about the flux and Gauss’s law here. In this solution, we'll use the formula of Gauss's law to calculate the flux through the surface we've been provided. The surface represents one of the cube's sides through which the flux will flow and hence we got our required solution.
Formula used:
ϕ=ε0q
Where, ϕ is the flux and q is the charge.
Complete step by step answer:
According to the question, we have a charge +10μC. And we can calculate the flux from the given charge by the help of Gauss’s law,
ϕ=ε0q
This flux will now be emitted in all directions at the same time. To find the flux through the given surface, imagine the charge is enclosed by a cube with a side of 10 cm. The flux through the cube will then be as follows:
ϕ=ε0q
Because the flux is distributed evenly, the flux through one surface will be 1/6th of the total flux, because the cube has six sides. Therefore, the flux through the one surface is given by,
ϕ=6ε0q
Now, substituting all the given values in above equation,
